题目内容
5．已知随机变量ξ服从正态分布B（1，22），若P（ξ≤2）=0.8，则P（0≤ξ≤2）=（ ）| A． | 1 | B． | 0.8 | C． | 0.6 | D． | 0.3 |
分析 随机变量ξ服从正态分布N（1，σ2），得到曲线关于x=1对称，根据曲线的对称性得到P（0≤ξ≤1）=0.3，从而得到所求．
解答 解：∵随机变量ξ服从正态分布N（1，σ2），
∴正态曲线的对称轴为μ=1，
∴P（ξ≥1）=P（ξ≤1）=0.5
又P（ξ≤2）=0.8
∴P（1≤ξ≤2）=0.3，
根据对称性得P（0≤ξ≤1）=0.3
∴P（0≤ξ≤2）=0.6，
故选：C．
点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查概率的性质，是一个基础题．
练习册系列答案
相关题目
12．某企业生产的一种产品的广告费用x（单位：万元）与销售额y（单位：万元）的统计数据如表：
（1）根据上述数据，求出销售额y（万元）关于广告费用x（万元）的线性回归方程；
（2）如果企业要求该产品的销售额不少于36万元，则投入的广告费用应不少于多少万元？
（参考数值：$\sum_{i=1}^{5}{x}_{i}=15$，$\sum_{i=1}^{5}{y}_{i}=150$，$\sum_{i=1}^{5}{x}_{i}{y}_{i}=570$，$\sum_{i=1}^{5}{{x}_{i}}^{2}=55$，$\sum_{i=1}^{5}{{y}_{i}}^{2}=6000$．
回归直线的斜率和截距的最小二乘估计公式分别为：$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$，$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$）
| 广告费用x | 1 | 2 | 3 | 4 | 5 |
| 销售额y | 10 | 15 | 25 | 45 | 55 |
（2）如果企业要求该产品的销售额不少于36万元，则投入的广告费用应不少于多少万元？
（参考数值：$\sum_{i=1}^{5}{x}_{i}=15$，$\sum_{i=1}^{5}{y}_{i}=150$，$\sum_{i=1}^{5}{x}_{i}{y}_{i}=570$，$\sum_{i=1}^{5}{{x}_{i}}^{2}=55$，$\sum_{i=1}^{5}{{y}_{i}}^{2}=6000$．
回归直线的斜率和截距的最小二乘估计公式分别为：$\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$，$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$）
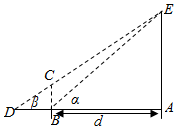为了培养学生的数学建模和应用能力，某校组织了一次实地测量活动，如图，假设待测量的树木AE的高度H（m），垂直放置的标杆BC的高度h=4m，仰角∠ABE=α，∠ADE=β（D，C，E三点共线），试根据上述测量方案，回答如下问题：
14．在区间[0，4]内随机选一个实数x，该实数恰好在区间[1，3]内的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |