题目内容
如图,四棱柱 中,
中, .
. 为平行四边形,
为平行四边形, ,
,  ,
,  分别是
分别是 与
与 的中点.
的中点.
(1)求证: ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
(1)见解析 (2) 
解析试题分析:(1) 先证明△ADE为正△,再利用余弦定理可求CE ,然后证明出CE⊥DE ,CE⊥DD1,最后得到CE⊥平面DD1E, 即可证明出CE⊥DF. (2)先建立以直线AB, AA1分别为 轴,
轴,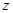 轴建立空间直角坐标系,然后根据点坐标求出法向量
轴建立空间直角坐标系,然后根据点坐标求出法向量 ,
, ,再利用夹角公式求出二面角
,再利用夹角公式求出二面角 的平面角的余弦值
的平面角的余弦值 .
.
(1)AD="AE," ∠DAB=60° ∴△ADE为正△
在△CDE中,由余弦定理可求CE= .
.
又 .由勾股定理逆定理知CE⊥DE
.由勾股定理逆定理知CE⊥DE
又DD1⊥平面ABCD, CE 平面ABCD. ∴CE⊥DD1
平面ABCD. ∴CE⊥DD1
∴CE⊥平面DD1E, 又DF 平面DD1E. ∴CE⊥DF.
平面DD1E. ∴CE⊥DF.
(2)以直线AB, AA1分别为 轴,
轴,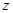 轴建立空间直角坐标系,由题设A(0,0,0), E(1,0,0),
轴建立空间直角坐标系,由题设A(0,0,0), E(1,0,0),
D1( ), C
), C
可求平面AEF的一个法向量为
平面CEF的一个法向量为
∴平面角 满足
满足
又 为纯角 ∴
为纯角 ∴
注:本题(1)也可建坐标直接证明.(2)的坐标系建法不唯一.
考点:余弦定理;勾股定理逆定理;线面垂直的性质与判定定理;法向量;夹角公式.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 的直径AB=3,点C为
的直径AB=3,点C为 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点. 平面VAC;
平面VAC;
 中,
中, 分别为棱
分别为棱 的中点,已知
的中点,已知 ,
,
 平面
平面 ;
;
 平面
平面 .
. 中,
中, .
.  在对角线
在对角线 上移动,求证:
上移动,求证: ⊥
⊥ ;
; 中点时,求点
中点时,求点 的距离。
的距离。 

 中,
中, .
.  ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使得平面
,使得平面
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点. 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 ⊥A1C.
⊥A1C.
 中,侧棱垂直于底面,
中,侧棱垂直于底面, ,
, ,
, 、
、 分别为
分别为 、
、 的中点.
的中点. 平面
平面 ;
; 平面
平面 ;
; 的体积.
的体积.
 ,求AB和CD所成角的余弦值.
,求AB和CD所成角的余弦值.