题目内容
(满分14分)如图在三棱锥 中,
中, 分别为棱
分别为棱 的中点,已知
的中点,已知 ,
,
求证(1)直线 平面
平面 ;
;
(2)平面
 平面
平面 .
.
证明见解析.
解析试题分析:(1)本题证明线面平行,根据其判定定理,需要在平面 内找到一条与
内找到一条与 平行的直线,由于题中中点较多,容易看出
平行的直线,由于题中中点较多,容易看出 ,然后要交待
,然后要交待 在平面
在平面 外,
外,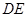 在平面
在平面 内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得
内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得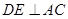 ,因此考虑能否证明
,因此考虑能否证明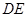 与平面
与平面 内的另一条与
内的另一条与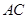 相交的直线垂直,由已知三条线段的长度,可用勾股定理证明
相交的直线垂直,由已知三条线段的长度,可用勾股定理证明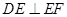 ,因此要找的两条相交直线就是
,因此要找的两条相交直线就是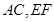 ,由此可得线面垂直.
,由此可得线面垂直.
试题解析:(1)由于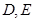 分别是
分别是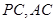 的中点,则有
的中点,则有 ,又
,又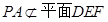 ,
,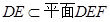 ,所以
,所以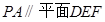 .
.
(2)由(1) ,又
,又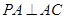 ,所以
,所以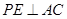 ,又
,又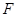 是
是 中点,所以
中点,所以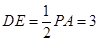 ,
, ,
, 又
又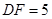 ,所以
,所以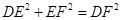 ,所以
,所以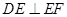 ,
, 是平面
是平面 内两条相交直线,所以
内两条相交直线,所以 ,又
,又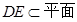
 ,所以平面
,所以平面
 平面
平面 .
.
【考点】线面平行与面面垂直.

练习册系列答案
相关题目
 .
. 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.
 中,底面
中,底面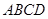 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, 是
是 的中点.
的中点. 平面
平面 ;
; 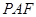 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 为正方形,
为正方形, 平面
平面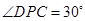 ,
, 于点
于点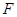 ,
, ,交
,交 于点
于点 .
.
 平面
平面 ;
;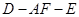 的余弦值.
的余弦值.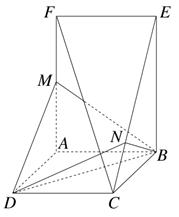
 中,
中, .
. 为平行四边形,
为平行四边形, ,
,  ,
,  分别是
分别是 与
与 的中点.
的中点.
 ;
; 的平面角的余弦值.
的平面角的余弦值. 中,
中, 底面
底面 ,
,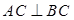 ,
, 为
为 的中点,
的中点,  为
为 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 与平面
与平面 成角的正弦值;
成角的正弦值; 在线段
在线段 上,且
上,且 ,
, 平面
平面 ,求实数
,求实数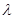 的值.
的值. 、
、 、
、 是直线,
是直线,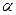 是平面,给出下列命题:①若
是平面,给出下列命题:①若 ,
, ,则
,则 ;
; ,
, ;③若
;③若 ,
, ,则
,则 ,
,