题目内容
16．有一智能机器人在平面上行进中始终保持与点F（1，0）的距离和到直线x=-1的距离相等，若机器人接触不到过点P（-1，0）且斜率为k的直线，求k的取值范围．分析 由抛物线的定义，求出机器人的轨迹方程，过点P（-1，0）且斜率为k的直线方程为y=k（x+1），代入y2=4x，利用判别式，即可求出k的取值范围．
解答 解：由题意可知机器人的轨迹为一抛物线，其轨迹方程为y2=4x，
过点P（-1，0）且斜率为k的直线方程为y=k（x+1），…（4分）
由题意知直线与抛物线无交点，即当直线位于图中阴影部分时，机器人是接触不到的；
联立消去y，得k2x2+（2k2-4）x+k2=0，则△=（2k2-4）2-4k4＜0，…（8分）
所以k2＞1，得k＞1或k＜-1．…（10分）
点评 本题考查抛物线的定义，考查直线与抛物线的位置关系，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．
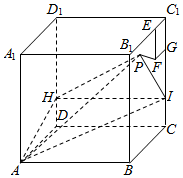如图所示，正方体ABCD-A1B1C1D1棱长为4，点H在棱DD1上，点I在棱CC1上，且HD=CI=1，在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1，侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍，则当点P运动时，三棱锥A-HPI的体积的最小值是（ ）
如图所示，正方体ABCD-A1B1C1D1棱长为4，点H在棱DD1上，点I在棱CC1上，且HD=CI=1，在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1，侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍，则当点P运动时，三棱锥A-HPI的体积的最小值是（ ）| A． | $\frac{2\sqrt{17}}{3}$ | B． | $\frac{25}{6}$ | C． | $\frac{2\sqrt{17}}{3}$（10-3$\sqrt{2}$） | D． | $\frac{20}{3}$-2$\sqrt{2}$ |
4．一个棱长为12的正四面体纸盒内放一个正方体，若正方体可以在纸盒内任意转动，则正方体的体积最大值是（ ）
| A． | 16$\sqrt{2}$ | B． | 6$\sqrt{2}$ | C． | 12$\sqrt{2}$ | D． | 32$\sqrt{2}$ |
11．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，短轴的一个端点为M，直线l：3x-4y=0交椭圆C于A，B两点，若|AF|+|BF|=4，点M到直线l的距离等于$\frac{4}{5}$，则椭圆C的离心率为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | $\frac{3}{2}$ | D． | $\frac{\sqrt{6}}{4}$ |
1．已知一正三棱台上底边长为3，下底边长为6，高为3，则此三棱台体积为（ ）
| A． | $\frac{{63\sqrt{3}}}{4}$ | B． | $\frac{{21\sqrt{3}}}{4}$ | C． | $\frac{{45\sqrt{3}}}{4}$ | D． | $\frac{{15\sqrt{3}}}{4}$ |