题目内容
8.已知圆C与两平行直线x-y=0及x-y-4=0都相切,且圆心C在直线x+y=0上,(1)求圆C的方程;
(2)若直线l:y=kx-2与圆C恒有两个不同的交点A和B,且$\overrightarrow{OA}•\overrightarrow{OB}>2$(其中O为原点),求k的取值范围.
分析 (1)利用平行线之间的距离求出圆的直径,设出圆心坐标,利用圆心到直线的距离,求出圆心坐标,可得圆的方程.
(2)联立直线和圆方程,利用韦达定理,结合$\overrightarrow{OA}•\overrightarrow{OB}>2$(其中O为原点),即可求k的取值范围.
解答 解:(1)由题意知⊙C的直径为两平行线 x-y=0及x-y-4=0之间的距离d=2R=$\frac{|0-(-4)|}{\sqrt{2}}$=2$\sqrt{2}$
∴解得R=$\sqrt{2}$,
由圆心C(a,-a)到 x-y=0的距离$\frac{|2a|}{\sqrt{2}}=\sqrt{2}$得a=±1,检验得a=1
∴⊙C的方程为(x-1)2+(y+1)2=2;
(2)直线l:y=kx-2与圆C,联立可得(1+k2)x2-(2+2k)x=0,
∴x1+x2=$\frac{2+2k}{1+{k}^{2}}$,x1x2=0
由$\overrightarrow{OA}•\overrightarrow{OB}>2$,得x1x2+y1y2>2,
∴x1x2+y1y2=(k2+1)x1x2-2k(x1+x2)+4>2.
于是k2+2k-1<0,即-1-$\sqrt{2}$<k<-1+$\sqrt{2}$.
点评 本题考查了圆方程的求法,考查了直线与圆的关系,正确运用韦达定理是关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
19.已知正方体ABD-A1B1C1D1的棱长为2,E,F分别是CC1,DD1的中点,点P在矩形C1D1FE的内部及其边界上运动,点Q在线段AD上运动,则线段PQ中点M的轨迹所形成的几何体的体积为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
13.如图,平行六面体ABCD-A1B1C1D1中,AC与BD交于点M,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{A{A_1}}$=$\overrightarrow c$,则$\overrightarrow{{B_1}M}$=( )


| A. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\overrightarrow c$ |
17.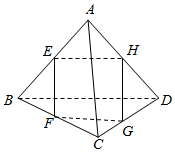 在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
 在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )| A. | 2对 | B. | 4对 | C. | 6对 | D. | 8对 |
18.对于函数f(x)在定义域内用二分法的求解过程中得到f(2015)<0,f(2016)<0,f(2017)>0,则下述描述正确的是( )
| A. | 函数f(x)在(2015,2016)内不存在零点 | |
| B. | 函数f(x)在(2016,2017)内不存在零点 | |
| C. | 函数f(x)在(2016,2017)内存在零点,并且仅有一个 | |
| D. | 函数f(x)在(2015,2016)内可能存在零点 |
 由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD中,E、F分别是棱BC、AD的中点,CF与DE是一对异面直线,在图形中适当的选取一点作出异面直线CF、DE的平行线,找出异面直线CF与DE成的角.(注:至少用四种方法)
由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD中,E、F分别是棱BC、AD的中点,CF与DE是一对异面直线,在图形中适当的选取一点作出异面直线CF、DE的平行线,找出异面直线CF与DE成的角.(注:至少用四种方法)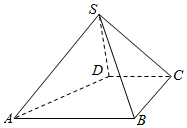 如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.