题目内容
7.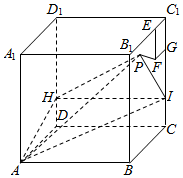 如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )
如图所示,正方体ABCD-A1B1C1D1棱长为4,点H在棱DD1上,点I在棱CC1上,且HD=CI=1,在侧面BCC1B1内以C1为一个顶点作边长为1的正方形EFGC1,侧面BCC1B1内动点P满足到平面CDD1C1距离等于线段PF长的$\sqrt{2}$倍,则当点P运动时,三棱锥A-HPI的体积的最小值是( )| A. | $\frac{2\sqrt{17}}{3}$ | B. | $\frac{25}{6}$ | C. | $\frac{2\sqrt{17}}{3}$(10-3$\sqrt{2}$) | D. | $\frac{20}{3}$-2$\sqrt{2}$ |
分析 建立空间直角坐标系,求出P的轨迹方程,确定三棱锥A-HPI的体积最小时,P的坐标,即可得出结论.
解答 
解:建立空间直角坐标系,如图所示
设P(x,4,z),则F(1,4,3),N(0,4,z),且4≥x≥0,4≥z≥0;
∵PN=$\sqrt{2}$PF,∴x=2(x-1)2+2(z-3)2,
化简得(x-$\frac{5}{4}$)2+(z-3)2=$\frac{9}{16}$
∴P为($\frac{5}{4}$,4,$\frac{9}{4}$)时,三棱锥A-HPI的体积最小.
∵A(4,0,0),H(0,0,1),I(0,4,1),
∴$\overrightarrow{AH}$=(-4,0,1),$\overrightarrow{AI}$=(-4,4,1),
设平面AHI的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{-4x+z=0}\\{-4x+4y+z=0}\end{array}\right.$,
∴$\overrightarrow{n}$=(1,0,4),
∵$\overrightarrow{AP}$=(-$\frac{11}{4}$,4
∴P到平面AHI的距离为$\frac{|-\frac{11}{4}+9|}{\sqrt{17}}$=$\frac{25}{4\sqrt{17}}$
∴三棱锥A-HPI的体积的最小值是$\frac{1}{3}×\frac{1}{2}×4×\sqrt{17}$×$\frac{25}{4\sqrt{17}}$=$\frac{25}{6}$
故选:B.
点评 本题考查了空间直角坐标系的应用问题,也考查了空间中的距离的最值问题,是较难的题目.

练习册系列答案
相关题目
20.设a>1,b>2,且ab=2a+b,则a+b的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$+1 | C. | 2$\sqrt{2}$+2 | D. | 2$\sqrt{2}$+3 |
19.已知正方体ABD-A1B1C1D1的棱长为2,E,F分别是CC1,DD1的中点,点P在矩形C1D1FE的内部及其边界上运动,点Q在线段AD上运动,则线段PQ中点M的轨迹所形成的几何体的体积为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
17.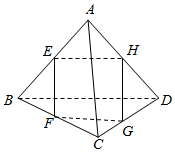 在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
 在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )
在如图所示的空间四边形ABCD中,E、F、G、H分别是AB,BC,CD,AD的中点,则图中共有多少对线面平行关系?( )| A. | 2对 | B. | 4对 | C. | 6对 | D. | 8对 |
 由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD中,E、F分别是棱BC、AD的中点,CF与DE是一对异面直线,在图形中适当的选取一点作出异面直线CF、DE的平行线,找出异面直线CF与DE成的角.(注:至少用四种方法)
由四个全等的等边三角形的封面几何体称为正四面体,如图,正四面体ABCD中,E、F分别是棱BC、AD的中点,CF与DE是一对异面直线,在图形中适当的选取一点作出异面直线CF、DE的平行线,找出异面直线CF与DE成的角.(注:至少用四种方法)