题目内容
11.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆C于A,B两点,若|AF|+|BF|=4,点M到直线l的距离等于$\frac{4}{5}$,则椭圆C的离心率为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{6}}{4}$ |
分析 设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,可得4=|AF|+|BF|=|AF′|+|BF|=2a.取M(0,b),由点M到直线l的距离为$\frac{4}{5}$,可得$\frac{|4b|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{4}{5}$,解得b=1.再利用离心率计算公式e=$\frac{c}{a}$,即可得出.
解答 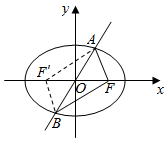 解:如图所示,设F′为椭圆的左焦点,连接AF′,BF′
解:如图所示,设F′为椭圆的左焦点,连接AF′,BF′
则四边形AFBF′是平行四边形,
∴4=|AF|+|BF|=|AF′|+|AF|=2a,∴a=2.
取M(0,b),
∵点M到直线l的距离为$\frac{4}{5}$,∴$\frac{|4b|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{4}{5}$,解得b=1.
∴e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查了椭圆的定义、标准方程及其性质、点到直线的距离公式,考查了计算能力,属于中档题.

练习册系列答案
相关题目
6.若M=tan$\frac{α}{2}$•sinα+cosα,N=tan$\frac{π}{8}$(tan$\frac{π}{8}$+2),则 M 和 N的大小关系是( )
| A. | M>N | B. | M<N | C. | M=N | D. | M和N无关 |
19.已知正方体ABD-A1B1C1D1的棱长为2,E,F分别是CC1,DD1的中点,点P在矩形C1D1FE的内部及其边界上运动,点Q在线段AD上运动,则线段PQ中点M的轨迹所形成的几何体的体积为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
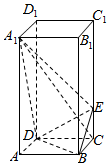 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.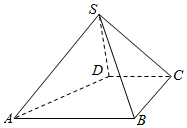 如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.