题目内容
已知数列{an}满足a1=0,a2=1,当n∈N*时,an+2=an+1+an.求证:数列{an}的第4m+1项(m∈N*)能被3整除.
(1)当m=1时,a4m+1=a5=a4+a3=(a3+a2)+(a2+a1)=(a2+a1)+2a2+a1=3a2+2a1=3+0=3.
即当m=1时,第4m+1项能被3整除.故命题成立.
(2)假设当m=k时,a4k+1能被3整除,
则当m=k+1时,
a4(k+1)+1=a4k+5=a4k+4+a4k+3
=2a4k+3+a4k+2=2(a4k+2+a4k+1)+a4k+2
=3a4k+2+2a4k+1.
显然,3a4k+2能被3整除,
又由假设知a4k+1能被3整除.
∴3a4k+2+2a4k+1能被3整除.
即当m=k+1时,a4(k+1)+1也能被3整除.命题也成立.
由(1)和(2)知,对于n∈N*,数列{an}中的第4m+1项能被3整除.

练习册系列答案
相关题目
 ≤2.
≤2. +
+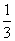 +…+
+…+ <n(n∈N*,n>1)时,第一步应验证不等式( )
<n(n∈N*,n>1)时,第一步应验证不等式( )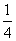 <3
<3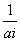 ,ci=
,ci=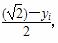 ,是否存在正整数N,当n≥N时,都有
,是否存在正整数N,当n≥N时,都有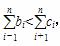 ,若存在,求出N的最小值并证明;若不存在,说明理由.
,若存在,求出N的最小值并证明;若不存在,说明理由.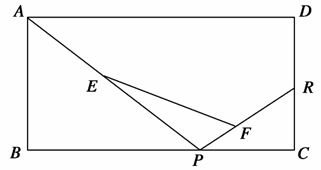
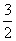 ,则线段CD的长为________.
,则线段CD的长为________.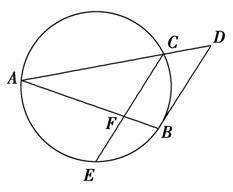
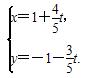 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为ρ=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为ρ=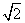 cos(θ+
cos(θ+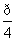 ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长.