题目内容
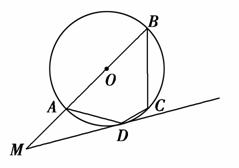
已知曲线C:y2=2x(y≥0),A1(x1,y1),A2(x2,y2),…,An(xn,yn),…是曲线C上的点,且满足0<x1<x2<…<xn<…,一列点Bi(ai,0)(i=1,2,…)在x轴上,且△Bi-1AiBi(B0是坐标原点)是以Ai为直角顶点的等腰直角三角形.
(1)求A1,B1的坐标;
(2)求数列{yn}的通项公式;
(3)令bi=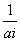 ,ci=
,ci=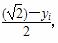 ,是否存在正整数N,当n≥N时,都有
,是否存在正整数N,当n≥N时,都有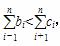 ,若存在,求出N的最小值并证明;若不存在,说明理由.
,若存在,求出N的最小值并证明;若不存在,说明理由.
(1)∵△B0A1B1是以A1为直角顶点的等腰直角三角形,
∴直线B0A1的方程为y=x.
由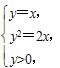 得x1=y1=2,即点A1的坐标为(2,2),进而得B1(4,0).
得x1=y1=2,即点A1的坐标为(2,2),进而得B1(4,0).
(2)根据△Bn-1AnBn和△BnAn+1Bn+1分别是以An和An+1为直角顶点的等腰直角三角形可得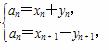
即xn+yn=xn+1-yn+1.(*)
∵An和An+1均在曲线C:y2=2x(y≥0)上,
 ∴数列{yn}是以y1=2为首项,2为公差的等差数列.
∴数列{yn}是以y1=2为首项,2为公差的等差数列.
∴其通项公式为yn=2n(n∈N*).
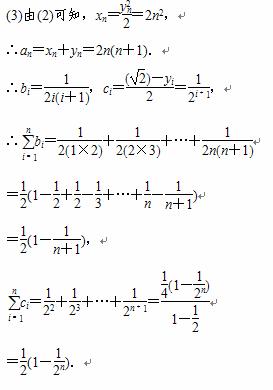
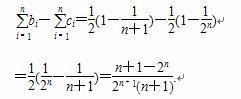 当n=1时,b1=c1不符合题意,当n=2时b2<c2符合题意,当n=3时,b3<c3,符合题意,猜想对于一切大于或等于2的自然数都有
当n=1时,b1=c1不符合题意,当n=2时b2<c2符合题意,当n=3时,b3<c3,符合题意,猜想对于一切大于或等于2的自然数都有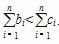 ,(*)
,(*)
观察知,欲证(*)式成立,只需证明n≥2时,n+1≤2n.
以下用数学归纳法证明,
①当n=2时,左边=3,右边=4,左边<右边;
②假设n=k(k≥2)时,k+1<2k,当n=k+1时,
左边=(k+1)+1<2k+1<2k+2k=2k+1=右边.
∴对于一切大于或等于2的正整数,都有n+1<2n,
即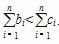 成立.
成立.
综上,满足题意的n的最小值为2.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 =1+i,则( )
=1+i,则( ) ,b=
,b= B.a=3,b=1
B.a=3,b=1

 D.
D.

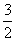 ) B.(-∞,-
) B.(-∞,-