题目内容
(1)化简f(α)=
;
(2)若tanα=2,求f(α)的值.
sin(
| ||
3cos(2π+α)+cos(
|
(2)若tanα=2,求f(α)的值.
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)由条件,利用诱导公式化简所给的式子,可得结果.
(2)由条件,利用同角三角函数的基本关系化简所给的式子,可得结果.
(2)由条件,利用同角三角函数的基本关系化简所给的式子,可得结果.
解答:
解:(1)由题意可得 f(α)=
=
=
.
(2)∵tanα=2,
∴f(α)═
=
=
=3.
sin(
| ||
3cos(2π+α)+cos(
|
| cosα+sin(π-α) |
| 3cosα-sinα |
| cosα+sinα |
| 3cosα-sinα |
(2)∵tanα=2,
∴f(α)═
| cosα+sinα |
| 3cosα-sinα |
| 1+tanα |
| 3-tanα |
| 1+2 |
| 3-2 |
点评:本题主要考查利用诱导公式、同角三角函数的基本关系进行化简求值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
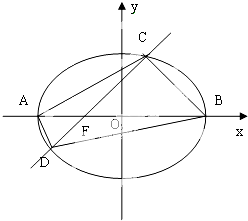 已知椭圆M:
已知椭圆M: 已知椭圆C:
已知椭圆C: 如图,已知角α的终边在第二象限,且与单位圆交于点P(m,
如图,已知角α的终边在第二象限,且与单位圆交于点P(m,