题目内容
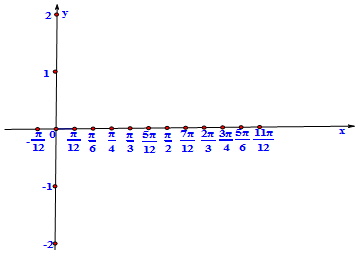
11. 函数f(x)=Acos(wx+φ)(A>0,W>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)值为( )
函数f(x)=Acos(wx+φ)(A>0,W>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)值为( )| A. | 0 | B. | 2-$\sqrt{2}$ | C. | 1 | D. | $\sqrt{2}$ |
分析 根据图象求出函数的解析式,结合三角函数的性质即可得到结论.
解答 解:由图象可得:A=2,周期T=8,
∴$\frac{2π}{8}=ω$,即ω=$\frac{π}{4}$.
图象过点(2,2),
即2=2cos($\frac{π}{4}×2+$φ)=-2sinφ
得:φ=-$\frac{π}{2}$+2kπ.
则f(x)=2cos($\frac{π}{4}x-\frac{π}{2}$)=2sin$\frac{π}{4}x$.
∵f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)=0.
那么:f(1)+f(2)+…+f(2017)=f(1)=2sin$\frac{π}{4}$=$\sqrt{2}$.
故选:D.
点评 本题考查了图象求出三角函数的解析式,和周期函数的计算.属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
1.sin(-375°)=( )
| A. | $\frac{\sqrt{3}-\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | -$\frac{\sqrt{6}+\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}+\sqrt{2}}{2}$ |
16. 如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是( )
如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是( )
 如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是( )
如图,已知一个八面体各棱长均为1,四边形ABCD为正方形,则下列命题中不正确的是( )| A. | 不平行的两条棱所在直线所成的角为60°或90° | |
| B. | 四边形AECF为正方形 | |
| C. | 点A到平面BCE的距离为$\frac{{\sqrt{6}}}{4}$ | |
| D. | 该八面体的顶点在同一个球面上 |
3.已知△ABC周长为6,a,b,c分别为角A,B,C的对边,且a,b,c成等比数列,则$\overrightarrow{BA}$•$\overrightarrow{BC}$的取值范围为( )
| A. | [2,18) | B. | ($\frac{3(\sqrt{5}-1)}{2}$,2] | C. | [2,$\frac{27-9\sqrt{5}}{2}$) | D. | (2,9-3$\sqrt{5}$) |