题目内容
已知命题“若存在x0≥4,不等式(x-a)•(x+1)≤2-a成立“的逆否命题为真,则实数a的取值范围是( )
A、[
| ||
B、(-∞,
| ||
C、[
| ||
D、(-∞,
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:命题“若存在x0≥4,不等式(x-a)•(x+1)≤2-a成立“的逆否命题为真,因此原命题也为真命题.于是存在x0≥4,不等式(x-a)•(x+1)≤2-a成立?a≥(x-
+1)min,x≥4.令f(x)=x-
+1,x≥4.利用导数研究其单调性极值最值即可得出.
| 2 |
| x |
| 2 |
| x |
解答:
解:命题“若存在x0≥4,不等式(x-a)•(x+1)≤2-a成立“的逆否命题为真,
因此原命题也为真命题.
∴存在x0≥4,不等式(x-a)•(x+1)≤2-a成立?a≥(x-
+1)min,x≥4.
令f(x)=x-
+1,x≥4.
∴f′(x)=1+
>0,
因此f(x)在[4,+∞)上单调递增,
∴当x=4时,函数f(x)取得最小值f(4)=
.
∴a≥
.
则实数a的取值范围是[
,+∞).
故选:A.
因此原命题也为真命题.
∴存在x0≥4,不等式(x-a)•(x+1)≤2-a成立?a≥(x-
| 2 |
| x |
令f(x)=x-
| 2 |
| x |
∴f′(x)=1+
| 2 |
| x2 |
因此f(x)在[4,+∞)上单调递增,
∴当x=4时,函数f(x)取得最小值f(4)=
| 9 |
| 2 |
∴a≥
| 9 |
| 2 |
则实数a的取值范围是[
| 9 |
| 2 |
故选:A.
点评:本题考查了利用导数研究其单调性极值最值、原没有与逆否命题的等价性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某大学生在22门考试中,所得分数如茎叶图所示,则此学生考试分数的极差与中位数之和为( )

| A、117 | B、118 |
| C、118.5 | D、119.5 |
运行如图所示的程序框图,则输出的所有实数对(x,y)所对应的点都在函数( )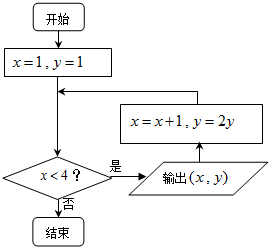

| A、f(x)=log2(x+1)的图象上 | ||
| B、f(x)=x2-2x+2的图象上 | ||
C、f(x)=
| ||
| D、f(x)=2x-1的图象上 |
下列命题正确的是( )
| A、垂直于同一直线的两条直线互相平行 |
| B、平行四边形在一个平面上的平行投影一定是平行四边形 |
| C、平面截正方体所得的截面图形可能是正六边形 |
| D、锐角三角形在一个平面上的平行投影不可能是钝角三角形 |
若函数f(x)对于任意的x∈R都有f(x+3)=-f(x+1),且f(3)=2015,则f(f(2015)-2]+1=( )
| A、-2015 | B、-2014 |
| C、2014 | D、2015 |