题目内容
设全集为U,集合A与集合B的关系如图,则下列说法正确的是( )


| A、对任意a∈A,都有a∉B |
| B、不存在b∈B,使b∈A |
| C、对任意c∈∁UA都有c∈B |
| D、存在d∈B,使d∈∁UA |
考点:Venn图表达集合的关系及运算
专题:集合
分析:根据Venn图,即可确定阴影部分对应的集合,根据集合元素和集合之间的关系即可得到结论.
解答:
解;A.当a∈A∩B时,a∈B,故A错误.
B.当b∈A∩B时,满足b∈B,且b∈A,故B错误
C.当c∈∁U(A∪B)时,c∉B,故C错误.
D.若d∈B∩(∁UA)时,满足d∈∁UA,
故选:D
B.当b∈A∩B时,满足b∈B,且b∈A,故B错误
C.当c∈∁U(A∪B)时,c∉B,故C错误.
D.若d∈B∩(∁UA)时,满足d∈∁UA,
故选:D
点评:本题主要考查集合的基本关系的判断,比较基础.

练习册系列答案
相关题目
A、B、C、D、E五人站成一排,如果A必须站在B的左边,则不同排法有( )
| A、24种 | B、60种 |
| C、90种 | D、120种 |
下列命题中正确的有( )
①函数y=
的单调递增区间是(-∞,0)∪(0,+∞)
②函数y=
的值域是R
③集合{
|0≤x≤3且x∈Z}={0,
,1,
}.
①函数y=
| 1 |
| x |
②函数y=
| 3 | x2 |
③集合{
| x |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
某校150名教职工中,有老年人20个,中年人50个,青年人80个,从中抽取30个作为样本.
①采用随机抽样法:抽签取出30个样本;
②采用系统抽样法:将教工编号为00,01,…,149,然后平均分组抽取30个样本;
③采用分层抽样法:从老年人,中年人,青年人中抽取30个样本.
下列说法中正确的是( )
①采用随机抽样法:抽签取出30个样本;
②采用系统抽样法:将教工编号为00,01,…,149,然后平均分组抽取30个样本;
③采用分层抽样法:从老年人,中年人,青年人中抽取30个样本.
下列说法中正确的是( )
| A、无论采用哪种方法,这150个教工中每一个被抽到的概率都相等 |
| B、①②两种抽样方法,这150个教工中每一个被抽到的概率都相等;③并非如此 |
| C、①③两种抽样方法,这150个教工中每一个被抽到的概率都相等;②并非如此 |
| D、采用不同的抽样方法,这150个教工中每一个被抽到的概率是各不相同的 |
若a<b<0,则下列不等式中成立的是( )
A、
| ||||
B、b+
| ||||
C、a+
| ||||
D、
|
一个各项均为正数的等比数列,其任何一项都等于它后面两项之和,则其公比是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
不等式(x-2)(x-1)<0的解集是( )
| A、{x|1<x<2} |
| B、{x|x<1或x>2} |
| C、{x|x<1} |
| D、{x|x>2} |
极坐标系中,过点(2,
)且与极轴垂直的直线方程为( )
| π |
| 3 |
A、ρsinθ=-
| ||
B、ρ=-
| ||
| C、ρ=-4cosθ | ||
| D、ρcosθ-1=0 |
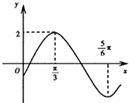
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则( )
| π |
| 2 |

A、ω=1,φ=
| ||
B、ω=1,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|