题目内容
求函数的值域:y=
(x>
).
| 2x2-x+1 |
| 2x-1 |
| 1 |
| 2 |
分析:利用分离常量的方法可得y=
=
=x+
(x>
),配凑基本不等式的形式,求解即可
| 2x2-x+1 |
| 2x-1 |
| x(2x-1)+1 |
| 2x-1 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
解答:解:y=
=
=x+
=x-
+
+
,
∵x>
,∴x-
>0,∴x-
+
≥2
=
,
当且仅当x-
=
时,即x=
时等号成立.
∴y≥
+
,
∴原函数的值域为:[
+
,+∞).
| 2x2-x+1 |
| 2x-1 |
| x(2x-1)+1 |
| 2x-1 |
| 1 |
| 2x-1 |
| 1 |
| 2 |
| ||
x-
|
| 1 |
| 2 |
∵x>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
x-
|
(x-
|
| 2 |
当且仅当x-
| 1 |
| 2 |
| ||
x-
|
1+
| ||
| 2 |
∴y≥
| 2 |
| 1 |
| 2 |
∴原函数的值域为:[
| 2 |
| 1 |
| 2 |
点评:本题主要考查了利用分离常量的方法把已知函数转化为利用基本不等式求解函数的最值的形式,利用基本不等式求解函数的最值时,一定要注意检验三个条件(一正,二定,三相等).

练习册系列答案
相关题目
 ,把函数y=g(x)的图象按向量
,把函数y=g(x)的图象按向量 =
= 平移后得到y=f(x)的图象.
平移后得到y=f(x)的图象. 的值域;
的值域; 时f(x)=0恒有解,求实数a的取值范围.
时f(x)=0恒有解,求实数a的取值范围.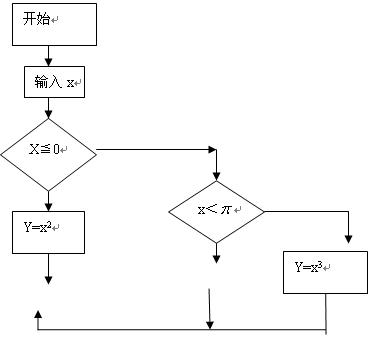
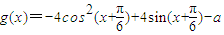 ,把函数y=g(x)的图象按向量
,把函数y=g(x)的图象按向量 =
=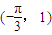 平移后得到y=f(x)的图象.
平移后得到y=f(x)的图象.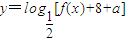 的值域;
的值域;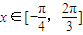 时f(x)=0恒有解,求实数a的取值范围.
时f(x)=0恒有解,求实数a的取值范围.