题目内容
已知函数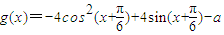 ,把函数y=g(x)的图象按向量
,把函数y=g(x)的图象按向量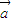 =
=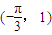 平移后得到y=f(x)的图象.
平移后得到y=f(x)的图象.(1)求函数
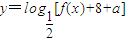 的值域;
的值域;(2)当
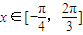 时f(x)=0恒有解,求实数a的取值范围.
时f(x)=0恒有解,求实数a的取值范围.
【答案】分析:(1)先将根据函数g(x)的图象按向量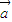 =
=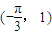 平移后得到y=f(x)的图象,求出y=f(x)的解析式,然后转化成关于cosx的二次函数,根据cosx的范围求出f(x)+8+a的范围,根据对数函数的单调性即可求出函数
平移后得到y=f(x)的图象,求出y=f(x)的解析式,然后转化成关于cosx的二次函数,根据cosx的范围求出f(x)+8+a的范围,根据对数函数的单调性即可求出函数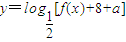 的值域;
的值域;
(2)根据 ,求出cosx的范围,从而求出f(x)的范围,要使f(x)=0恒有解,只需f(x)的最小值恒小于等于另且最大值恒大于等于零即可.
,求出cosx的范围,从而求出f(x)的范围,要使f(x)=0恒有解,只需f(x)的最小值恒小于等于另且最大值恒大于等于零即可.
解答:解:把函数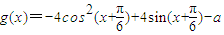
按向量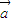
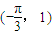
平移后得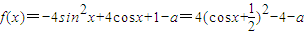 (2分)
(2分)
(1)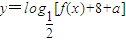 =
=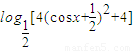 (3分)
(3分)
∵-1≤cosx≤1,∴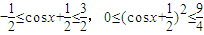 (5分)
(5分)
则函数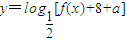 的值域为
的值域为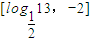 ;(7分)
;(7分)
(2)当 时,
时,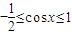 ,
,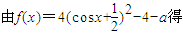
∴-4-a≤f(x)≤5-a(9分)∵f(x)=0恒有解,∴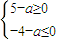 ,(11分)
,(11分)
即-4≤a≤5(12分)
点评:本题考查复合函数的单调性,以及函数的值域的求解,考查学生发现问题解决问题的能力,是基础题.
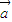 =
=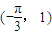 平移后得到y=f(x)的图象,求出y=f(x)的解析式,然后转化成关于cosx的二次函数,根据cosx的范围求出f(x)+8+a的范围,根据对数函数的单调性即可求出函数
平移后得到y=f(x)的图象,求出y=f(x)的解析式,然后转化成关于cosx的二次函数,根据cosx的范围求出f(x)+8+a的范围,根据对数函数的单调性即可求出函数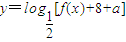 的值域;
的值域;(2)根据
 ,求出cosx的范围,从而求出f(x)的范围,要使f(x)=0恒有解,只需f(x)的最小值恒小于等于另且最大值恒大于等于零即可.
,求出cosx的范围,从而求出f(x)的范围,要使f(x)=0恒有解,只需f(x)的最小值恒小于等于另且最大值恒大于等于零即可.解答:解:把函数
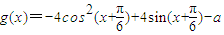
按向量
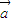
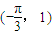
平移后得
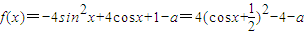 (2分)
(2分)(1)
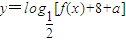 =
=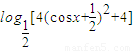 (3分)
(3分)∵-1≤cosx≤1,∴
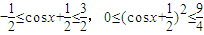 (5分)
(5分)则函数
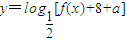 的值域为
的值域为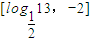 ;(7分)
;(7分)(2)当
 时,
时,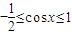 ,
,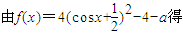
∴-4-a≤f(x)≤5-a(9分)∵f(x)=0恒有解,∴
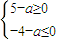 ,(11分)
,(11分)即-4≤a≤5(12分)
点评:本题考查复合函数的单调性,以及函数的值域的求解,考查学生发现问题解决问题的能力,是基础题.

练习册系列答案
相关题目
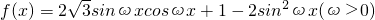 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.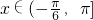 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间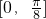 上的最小值.
上的最小值.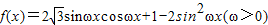 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.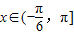 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移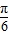 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间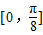 上的最小值.
上的最小值. ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π. ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值. ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.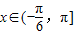 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.