题目内容
已知集合M={1，2，4}，N={a，b}，则M到N的映射共有（ ）个．
| A、5 | B、6 | C、8 | D、9 |
考点：映射
专题：常规题型,集合
分析：列出所有由M={1，2，4}到N={a，b}的映射．
解答：
解：由M={1，2，4}到N={a，b}的映射有：
①1，2，4→a，②1，2→a，4→b，③1，4→a，2→b，④2，4→a，1→b，⑤1→a，2，4→b，⑥2→a，1，4→b，⑦4→a，1，2→b，⑧1，2，4→b．
故共有8个．
故选：C．
①1，2，4→a，②1，2→a，4→b，③1，4→a，2→b，④2，4→a，1→b，⑤1→a，2，4→b，⑥2→a，1，4→b，⑦4→a，1，2→b，⑧1，2，4→b．
故共有8个．
故选：C．
点评：考查了映射的定义及列映射时的方法．
练习册系列答案
相关题目
已知向量
=（4，2），
=（6，y），且
∥
，则y=（ ）
| AB |
| CD |
| AB |
| CD |
| A、-3 | B、-2 | C、3 | D、2 |
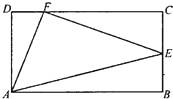如图所示，有一个长AB=4，宽BC=2的矩形木料ABCD，E为BC的中点，点F在边CD上．一木工师傅想在该木料上取满足∠EAF=| π |
| 3 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（0，
|
设L、m、n表示不同的直线，α、β、γ表示不同的平面，给出下列三个命题：正确的是（ ）
①若m∥L且m⊥α，则L⊥α
②若m∥L且m∥α，则L∥α
③若α∩β=L，β∩γ=m，γ∩α=n，则L∥m∥n．
①若m∥L且m⊥α，则L⊥α
②若m∥L且m∥α，则L∥α
③若α∩β=L，β∩γ=m，γ∩α=n，则L∥m∥n．
| A、0个 | B、1个 | C、2个 | D、3个 |
定义在R上的奇函数f（x）满足f（x+3）=f（x），当0＜x≤1时，f（x）=2x，则f（2）=（ ）
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
已知|
|=
，|
|=1，
与
的夹角为30°，则|
-2
|=（ ）
| a |
| 3 |
| b |
| a |
| b |
| a |
| b |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |