题目内容
11.已知函数f(x)=$\left\{\begin{array}{l}{2x+1,x>0}\\{0,x=0}\\{2x-1,x<0}\end{array}\right.$,则不等式f(x2-2)+f(x)<0的解集为(-2,1).分析 画出函数f(x)的,可知f(x)是定义域为R的奇函数也是增函数,即可求不等式f(x2-2)+f(x)<0的解集
解答 解:函数f(x)=$\left\{\begin{array}{l}{2x+1,x>0}\\{0,x=0}\\{2x-1,x<0}\end{array}\right.$,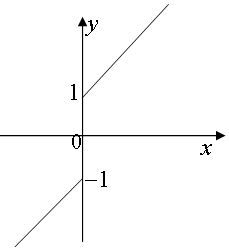
其图象如下:
∴f(x)是定义域为R的奇函数也是增函数,
不等式f(x2-2)+f(x)<0,
?f(x2-2)<f(-x)
等价于x2-2<-x,
解得:-2<x<1,
∴原不等式的解集为(-2,1).
故答案为:(-2,1).
点评 本题考查不等式的解法,利用了函数的奇偶性和单调性,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知平面向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a•({\overrightarrow a+\overrightarrow b})=3$,且$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$,则向量$\overrightarrow a$与$\overrightarrow b$夹角的余弦值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
3.已知ω>0,将函数f(x)=cosωx的图象向右平移$\frac{π}{2}$个单位后得到函数$g(x)=sin({ωx-\frac{π}{4}})$的图象,则ω的最小值是( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
1.若执行如图所示程序框图,则输出的s值为( )


| A. | -2016 | B. | 2016 | C. | -2017 | D. | 2017 |

 如图所示的流程图,当输入n的值为10时,则输出的S的值为30.
如图所示的流程图,当输入n的值为10时,则输出的S的值为30.