题目内容
20．将边长为1的正方形以其一边所在的直线为旋转轴旋转一周，所得几何体的侧面积是（ ）| A． | 8π | B． | 6π | C． | 4π | D． | 2π |
分析 所得几何体是以底面半径1，高为1的圆柱，由此能求出所得几何体的侧面积．
解答 解：将边长为1的正方形以其一边所在的直线为旋转轴旋转一周，
所得几何体是以底面半径1，高为1的圆柱，
∴所得几何体的侧面积S=2π×1=2π．
故选：D．
点评 本题考查几何体的侧面积的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10．数列$1，-\frac{3}{4}，\frac{1}{2}，-\frac{5}{16}，…$的一个通项公式为（ ）
| A． | ${（-1）^n}\frac{n+1}{2n}$ | B． | ${（-1）^{n+1}}\frac{2n-1}{2n}$ | C． | ${（-1）^{n+1}}\frac{n+1}{2^n}$ | D． | ${（-1）^{n+1}}\frac{2n-1}{2^n}$ |
5．（x3-$\frac{2}{x}$）4的展开式中的常数项为（ ）
| A． | 32 | B． | 64 | C． | -32 | D． | -64 |
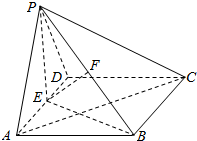如图，已知平面PAD⊥平面ABCD，ABCD为矩形，PA=PD，AD=$\sqrt{2}$AB，E是线段AD的中点，F是线段PB的中点．