Question

6．已知点P（x，y）在圆x²+y²-6x-6y+14=0上．
（1）求$\frac{y}{x}$的最大值和最小值；
（2）求x²+y²+2x+3的最大值与最小值．

Answer 1

分析 （1）求得已知圆的圆心和半径，设k=$\frac{y}{x}$，即kx-y=0，则圆心到直线的距离d≤r，加上即可得到最值；
（2）x²+y²+2x+3=（x+1）²+y²+2表示点（x，y）与A（-1，0）的距离的平方加上2，连接AC，交圆C于B，延长AC，交圆于D，可得AB最短，AD最长，加上即可得到所求最值．

解答 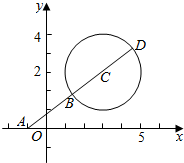解：（1）圆x²+y²-6x-6y+14=0即为（x-3）²+（y-3）²=4，
可得圆心为C（3，3），半径为r=2，
设k=$\frac{y}{x}$，即kx-y=0，
则圆心到直线的距离d≤r，
即$\frac{|3k-3|}{\sqrt{1+{k}^{2}}}$≤2，
平方得5k²-18k+5≤0，
解得$\frac{9-2\sqrt{14}}{5}$≤k≤$\frac{9+2\sqrt{14}}{5}$，
故$\frac{y}{x}$的最大值是$\frac{9+2\sqrt{14}}{5}$，最小值为$\frac{9-2\sqrt{14}}{5}$；
（2）x²+y²+2x+3=（x+1）²+y²+2
表示点（x，y）与A（-1，0）的距离的平方加上2，
连接AC，交圆C于B，延长AC，交圆于D，
可得AB为最短，且为|AC|-r=$\sqrt{16+9}$-2=3，
AD为最长，且为|AC|+r=5+2=7，
则x²+y²+2x+3 的最大值为7²+2=51，
x²+y²+2x+3的最小值为3²+2=11．

点评 本题主要考查直线和圆的方程的应用，根据圆心到直线的距离和半径之间的关系以及连接圆外一点与圆心的直线与圆的交点，取得最值是解决本题的关键．