题目内容
已知椭圆 经过点
经过点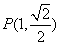 ,且两焦点与短轴的两个端点的连线构成一正方形. (12分)
,且两焦点与短轴的两个端点的连线构成一正方形. (12分)
(1)求椭圆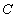 的方程;
的方程;
(2)直线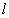 与椭圆
与椭圆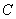 交于
交于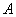 ,
,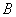 两点,若线段
两点,若线段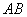 的垂直平分线经过点
的垂直平分线经过点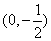 ,求
,求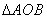
( 为原点)面积的最大值.
为原点)面积的最大值.
(1)∵椭圆 的两焦点与短轴的两个端点的连线构成正方形,
的两焦点与短轴的两个端点的连线构成正方形,
∴ , ∴
, ∴ , 2分
, 2分
又∵椭圆经过点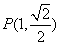 ,代入可得
,代入可得 ,
,
∴故所求椭圆方程为 4分
4分
(2)设 因为
因为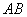 的垂直平分线通过点
的垂直平分线通过点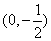 , 显然直线
, 显然直线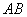 有斜率,
有斜率,
当直线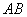 的斜率为
的斜率为 时,则
时,则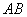 的垂直平分线为
的垂直平分线为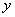 轴,此时
轴,此时
所以 ,因为
,因为 ,所以
,所以

所以 ,当且仅当
,当且仅当 时,
时, 取得最大值为
取得最大值为 , 6分
, 6分
当直线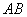 的斜率不为
的斜率不为 时,则设
时,则设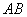 的方程为
的方程为
所以 ,代入得到
,代入得到
当 , 即
, 即

方程有两个不同的解又 ,
,
所以 ,又
,又 ,化简得到
,化简得到
 -----8分
-----8分
代入 ,得到
,得到
又原点到直线的距离为

所以
考虑到 且
且 化简得到
化简得到 10分
10分
因为 ,所以当
,所以当 时,即
时,即 时,
时, 取得最大值
取得最大值 .
.
综上,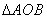 面积的最大值为
面积的最大值为 12分
12分

练习册系列答案
相关题目
 在
在 上的最大值与最小值
上的最大值与最小值 A=45°,C=60°,则BC=
A=45°,C=60°,则BC=  B.
B.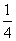 C.
C.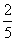 D .
D .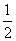
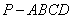 中,
中, ,底面
,底面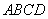 为梯形,
为梯形,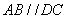 ,
,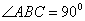 ,且
,且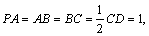
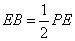 .(10分)
.(10分)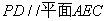 ;
;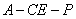 的余弦值.
的余弦值.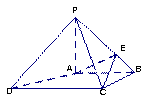
 ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 在R上开导,且
在R上开导,且 ,若
,若 ,则不等式
,则不等式 的解集为( )
的解集为( ) B.
B.  C.
C.  D.
D. 
 中,若
中,若 ,则
,则 角的等腰三角形
角的等腰三角形 则P的轨迹一定通过△ABC的 ( )
则P的轨迹一定通过△ABC的 ( )