题目内容
如图,四棱锥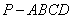 中,
中, ,底面
,底面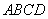 为梯形,
为梯形,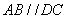 ,
,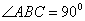 ,且
,且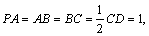
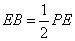 .(10分)
.(10分)
(1)求证: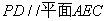 ;
;
(2)求二面角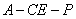 的余弦值.
的余弦值.
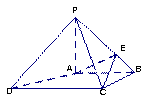
(1)连结 ,交
,交 于点
于点 ,连结
,连结 , ∵
, ∵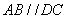 ,
, , ∴
, ∴
又 ∵ , ∴
, ∴ ∴ 在△BPD中,
∴ 在△BPD中, 

 ∴
∴ ∥平面
∥平面 ----------------4分
----------------4分
(2)方法一:以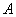 为原点,
为原点, 所在直线分别为
所在直线分别为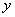 轴、
轴、 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.


设 ,则
,则 ,
, ,
,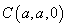 ,
, ,
, .
.
设 为平面
为平面 的一个法向量,
的一个法向量,
则 ,
, ,∴
,∴ ,
,
解得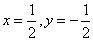 ,∴
,∴ .
.
设 为平面
为平面 的一个法向量,则
的一个法向量,则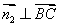 ,
, ,
,
又 ,
,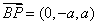 ,∴
,∴ ,
,
解得 ,∴
,∴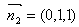

∴二面角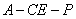 的余弦值为
的余弦值为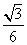 . -------------------10分
. -------------------10分
方法二:在等腰Rt 中,取
中,取 中点
中点 ,连结
,连结 ,则
,则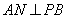

∵面 ⊥面
⊥面 ,面
,面
 面
面 =
= ,∴
,∴ 平面
平面 .
.
在平面 内,过
内,过 作
作 直线
直线 于
于 ,连结
,连结 ,由
,由 、
、 ,
,
得 平面
平面 ,故
,故 .
.
∴ 就是二面角
就是二面角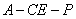 的平面角.
的平面角.
在 中,设
中,设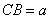 ,
, ,
, ,
,
 ,
, ,
,
由 ,
, 可知:
可知: ∽
∽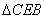 ,
,
∴ , 代入解得:
, 代入解得: .
.
在 中,
中, ,
,
∴ ,
, .
.
∴二面角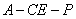 的余弦值为
的余弦值为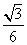 .-------------------10分
.-------------------10分

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 的单调递减区间为____________.
的单调递减区间为____________.
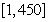 的人做问卷
的人做问卷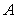 ,编号落入区间
,编号落入区间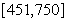 的人做问卷
的人做问卷 ,其余的人做问卷
,其余的人做问卷 ,则抽到的人中,做问卷
,则抽到的人中,做问卷 ,则
,则 =( )
=( ) C.
C. D .
D .
 经过点
经过点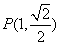 ,且两焦点与短轴的两个端点的连线构成一正方形. (12分)
,且两焦点与短轴的两个端点的连线构成一正方形. (12分)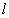 与椭圆
与椭圆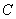 交于
交于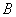 两点,若线段
两点,若线段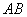 的垂直平分线经过点
的垂直平分线经过点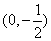 ,求
,求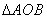
 为原点)面积的最大值.
为原点)面积的最大值. ,执行如右图所示的程序框图,则输出的x不小于55的概率为 ( )
,执行如右图所示的程序框图,则输出的x不小于55的概率为 ( ) B.
B. C.
C. D.
D.
 为等差数列
为等差数列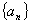 的前n项和,
的前n项和, ,则
,则 与
与 的等比中项为( )A.
的等比中项为( )A. B.
B. C.
C. D.
D.
 ( )
( )