题目内容
已知函数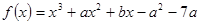 在
在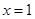 处取得极大值
处取得极大值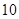 ,则
,则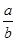 的值为( )
的值为( )
A. | B.-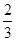 | C.-2或一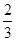 | D.不存在 |
B
解析试题分析::∵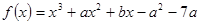 ,∴f′(x)=3x2+2ax+b,
,∴f′(x)=3x2+2ax+b,
又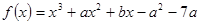 在x=1处取得极大值10,
在x=1处取得极大值10,
∴f′(1)=3+2a+b=0,f(1)=1+a+b-a2-7a=10,
∴a2+8a+12=0,
∴a=-2,b=1或a=-6,b=9.
当a=-2,b=1时,f′(x)=3x2-4x+1=(3x-1)(x-1),
当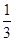 <x<1时,f′(x)<0,当x>1时,f′(x)>0,
<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在x=1处取得极小值,与题意不符;
当a=-6,b=9时,f′(x)=3x2-12x+9=3(x-1)(x-3),
当x<1时,f′(x)>0,当<x<3时,f′(x)<0,
∴f(x)在x=1处取得极大值,符合题意;
∴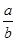 =-
=-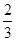 ,故选B。
,故选B。
考点:利用导数研究函数的极值。
点评:中档题,函数的极值点处的导数值为0.本题解答中,a,b有两组解,注意检验验证,合理取舍。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 ,则
,则 = ( )
= ( )
A. | B. |
C. | D. |
由曲线 与直线
与直线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A. | B. | C. | D. |
关于 的函数
的函数 的极值点的个数有( )
的极值点的个数有( )
| A.2个 | B.1个 | C.0个 | D.由 确定 确定 |
若函数 的导函数
的导函数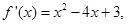 则函数
则函数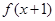 的单调递减区间是( )
的单调递减区间是( )
A.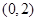 | B.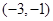 | C.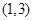 | D.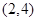 |
函数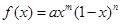 在区间
在区间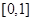 上的图像如图所示,则
上的图像如图所示,则 、
、 的值可能是( )
的值可能是( )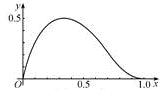
A.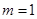 , , |
B.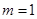 , ,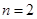 |
C. , , |
D. , , |
已知函数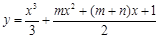 的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0, 1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数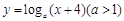 的图象上存在区域D内的点,则实数a的取值范围为( )
的图象上存在区域D内的点,则实数a的取值范围为( )
A.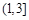 | B.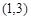 | C. | D.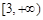 |
已知点 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 取值范围是
取值范围是
A.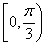 | B. | C.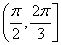 | D. |
在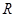 上可导的函数
上可导的函数 的图形如图所示,则关于
的图形如图所示,则关于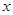 的不等式
的不等式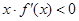 的解集为( )
的解集为( )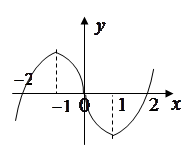
A.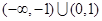 | B.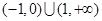 |
C.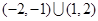 | D.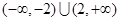 |