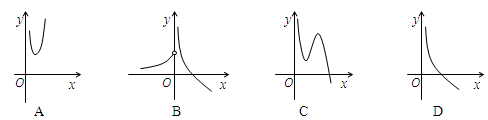题目内容
函数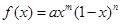 在区间
在区间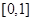 上的图像如图所示,则
上的图像如图所示,则 、
、 的值可能是( )
的值可能是( )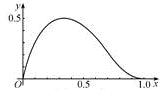
A.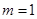 , , |
B.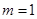 , ,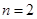 |
C. , , |
D. , , |
B
解析试题分析:原函数的极大值点小于0.5.把答案代入验证看哪个对应的极值点符合要求即可得出答案.解:由于本题是选择题,可以用代入法来作,由图得,原函数的极大值点小于0.5.当m=1,n=1时,f(x)=ax(1-x)=-a(x-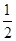 )2+
)2+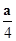 .在x=
.在x=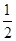 处有最值,故A错;当m=1,n=2时,f(x)=axm(1-x)n=ax(1-x)2=a(x3-2x2+x),所以f'(x)=a(3x-1)(x-1),令f'(x)=0⇒x=
处有最值,故A错;当m=1,n=2时,f(x)=axm(1-x)n=ax(1-x)2=a(x3-2x2+x),所以f'(x)=a(3x-1)(x-1),令f'(x)=0⇒x=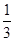 ,x=1,即函数在x=
,x=1,即函数在x=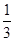 处有最值,故B对;当m=2,n=1时,f(x)=axm(1-x)n=ax2(1-x)=a(x2-x3),有f'(x)=a(2x-3x2)=ax(2-3x),令f'(x)=0⇒x=0,x=
处有最值,故B对;当m=2,n=1时,f(x)=axm(1-x)n=ax2(1-x)=a(x2-x3),有f'(x)=a(2x-3x2)=ax(2-3x),令f'(x)=0⇒x=0,x=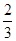 ,即函数在x=
,即函数在x=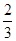 处有最值,故C错;当m=3,n=1时,f(x)=axm(1-x)n=ax3(1-x)=a(x3-x4),有f'(x)=ax2(3-4x),令f'(x)=0,⇒x=0,x=
处有最值,故C错;当m=3,n=1时,f(x)=axm(1-x)n=ax3(1-x)=a(x3-x4),有f'(x)=ax2(3-4x),令f'(x)=0,⇒x=0,x=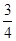 ,即函数在x=
,即函数在x=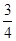 处有最值,故D错.故选 B
处有最值,故D错.故选 B
考点:函数的最值(极值)点与导函数之间的关系
点评:本题主要考查函数的最值(极值)点与导函数之间的关系.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.本本题考查利用极值求对应变量的值.可导函数的极值点一定是导数为0的点,但导数为0的点不一定是极值点

已知 是定义在
是定义在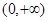 上的非负可导函数,且满足
上的非负可导函数,且满足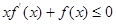 .对任意正数
.对任意正数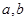 ,若
,若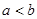 ,则必有( )
,则必有( )
A.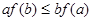 | B.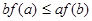 |
C.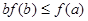 | D.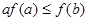 |
函数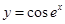 的导数是( )
的导数是( )
A.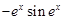 | B.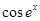 | C.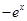 | D.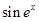 |
设函数 的最大值为3,则
的最大值为3,则 的图象的一条对称轴的方程是 ( )
的图象的一条对称轴的方程是 ( )
A. | B. |
C. | D. |
已知函数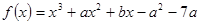 在
在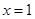 处取得极大值
处取得极大值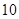 ,则
,则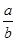 的值为( )
的值为( )
A. | B.-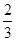 | C.-2或一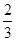 | D.不存在 |
设函数f(x)在 处可导,则
处可导,则 等于( )
等于( )
A. | B. | C.- | D.- |
已知函数 在
在 处取极值
处取极值 ,则
,则 =( )
=( )
| A.9 | B. | C. | D. |
已知函数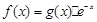 在
在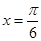 处有极值,则函数
处有极值,则函数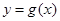 的图象可能是( )
的图象可能是( )
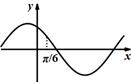
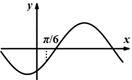

| A. | B. | C. | D. |
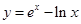 的图象是( )
的图象是( )