题目内容
1.曲线的参数方程是$\left\{\begin{array}{l}{x=1-\frac{1}{t}}\\{y=1-{t}^{2}}\end{array}\right.$(t是参数,t≠0),它的普通方程是( )| A. | (x-1)2(y-1)=1(y<1) | B. | y=$\frac{x(x-2)}{(x-1)^{2}}$(x≠1) | C. | y=$\frac{1}{1-{x}^{2}}$-1(y<1) | D. | y=$\frac{x}{1-{x}^{2}}$-1(y<1) |
分析 曲线的参数方程消去参数,能求出曲线的普通方程.
解答 解:∵曲线的参数方程是$\left\{\begin{array}{l}{x=1-\frac{1}{t}}\\{y=1-{t}^{2}}\end{array}\right.$(t是参数,t≠0),
∴消去参数,得曲线的普通方程为:
y=1-($\frac{1}{1-x}$)2=$\frac{x(x-2)}{(x-1)^{2}}$(x≠1).
故选:B.
点评 本题考查曲线的参数方程继普通方程的求法,考查参数方程、直角坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
20.直线l经过原点O和点P(1,1),则其斜率为( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
16.把数列{2n+1}(n∈N*)依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,…循环,分别:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),…,则第120个括号内各数之和为( )
| A. | 2312 | B. | 2392 | C. | 2472 | D. | 2544 |
13.函数$y=x+\frac{1}{4x}({x>0})$取得最小值时,x的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
10.若x,y且x+y>2,则$\frac{1+y}{x}$和$\frac{1+x}{y}$的值满足( )
| A. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都大于2 | B. | $\frac{1+y}{x}$和$\frac{1+x}{y}$都小于2 | ||
| C. | $\frac{1+y}{x}$和$\frac{1+x}{y}$中至少有一个小于2 | D. | 以上说法都不对 |
11.等差数列{an}的前n项和为Sn,已知a19+2a20+a21=4,则S39=( )
| A. | 38 | B. | 39 | C. | 20 | D. | 19 |
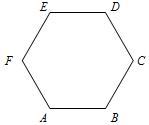 如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.
如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.