Question

已知椭圆4x²+y²=1及直线y=x+m.

(1)当直线和椭圆有公共点时,求实数m的取值范围;

(2)求被椭圆截得的最长弦所在的直线方程.

Answer 1

解：(1)由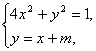得5x²+2mx+m²-1=0.

因为直线与椭圆有公共点,

所以Δ=4m²-20(m²-1)≥0.

解得

(2)设直线与椭圆交于A(x₁,y₁)、B(x₂,y₂),

由(1),知5x²+2mx+m²-1=0,

由根与系数的关系得x₁+x₂=,x₁x₂=(m²-1).设弦长为d,

所以

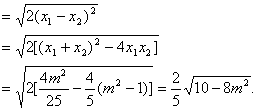
所以当m=0时，d最大,此时直线方程为y=x.

绿色通道：

判断直线与椭圆的交点情况就是要联立方程组,消去x(或y)转化为关于y(或x)的一元二次方程,利用判别式求解.在第(1)问中Δ≥0,即可求出m的取值范围.第(2)问求弦长最大时的直线方程,根据根与系数的关系和弦长公式,将弦长表示成关于m的函数,求出当弦长最长时的m值,从而确定直线方程.