题目内容
4．若不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{y≤kx+3}\\{0≤x≤3}\end{array}\right.$表示的区域为一个锐角三角形及其内部，则实数k的范围是（0，1）．分析 由题意作出其平面区域，求出k的临界值，从而结合图象写出实数k的取值范围．
解答 解：由题意作出其平面区域，
当直线y=kx+3与AB重合时，k=0，是直角三角形，
当直线y=kx+3与AD重合时，k=1，是直角三角形；
故若区域为一个锐角三角形及其内部，
则0＜k＜1；
故答案为：（0，1）．
点评 本题考查了简单线性规划，作图要细致认真，利用临界值求取值范围，属于中档题．
练习册系列答案
相关题目
9．设△ABC的内角A，B，C所对的边分别是a，b，c，若AB边上的高为$\frac{c}{2}$，且a2+b2=2$\sqrt{2}$ab，则C=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
16．若存在实数x=x0，使得不等式ax＞a-1不成立，则实数a的取值范围是（ ）
| A． | （-∞，0） | B． | （0，+∞） | C． | （-∞，0）∪（0，+∞） | D． | （-∞，+∞） |
11．记函数f（x）的导函数为f′（x），若f（x）对应的曲线在点（x0，f（x0））处的切线方程为y=-x+1，则（ ）
| A． | f′（x0）=2 | B． | f′（x0）=1 | C． | f′（x0）=0 | D． | f′（x0）=-1 |
，
，
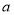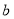是正数，求证：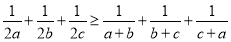
．