题目内容
19.已知AB,BC,CD为空间中不在同一平面内的三条线段,AB,BC,CD的中点分别为P,Q,R,PQ=2,QR=$\sqrt{5}$,PR=3,则AC与BD所成的角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | 0 |
分析 由已知得PQ2+QR2=PR2,AC∥PQ,BD∥QR,从而AC⊥BD,由此能求出AC与BD所成的角的余弦值.
解答  解:连结AC、BD、PQ、RQ、PR.
解:连结AC、BD、PQ、RQ、PR.
在△PQR中,∵PQ=2,QR=$\sqrt{5}$,PR=3,
∴PQ2+QR2=PR2,
∴PQ⊥QR,
∵AB,BC,CD的中点分别为P,Q,R,
∴AC∥PQ,BD∥QR,
∴AC⊥BD,
∴AC与BD所成的角的余弦值为0.
故选:D.
点评 本题考查两异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
7.设全集为R,集合A={y|y>2},B={x|-1≤x≤4},则(∁RA)∩B=( )
| A. | (2,4] | B. | [-1,2] | C. | [-1,4] | D. | (4,+∞) |
9.输人N的值为5,按如图所示的程序框图运行后,输出的结果是( )


| A. | $\frac{24}{25}$ | B. | $\frac{35}{36}$ | C. | $\frac{48}{49}$ | D. | $\frac{63}{64}$ |

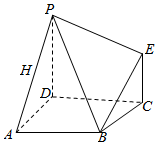 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2. 已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.
已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.