题目内容
已知函数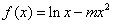 ,
,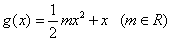 ,令
,令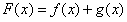 。
。
(Ⅰ)当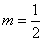 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于 的不等式
的不等式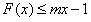 恒成立,求整数
恒成立,求整数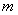 的最小值;
的最小值;
.【解析】解:⑴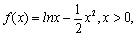
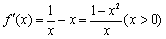 ……………………2分
……………………2分
由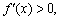 得
得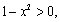 又
又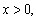 所以
所以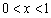 .所以
.所以 的单增区间为
的单增区间为 . ………4分
. ………4分
(2)方法一:令
所以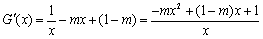 .………………………6分
.………………………6分
当 时,因为
时,因为 ,所以
,所以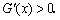 所以
所以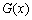 在
在 上是递增函数,
上是递增函数,
又因为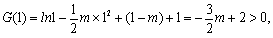
所以关于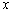 的不等式
的不等式 不能恒成立. ………………………8分
不能恒成立. ………………………8分
当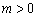 时,
时,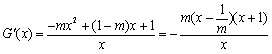 .
.
令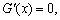 得
得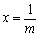 ,所以当
,所以当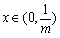 时,
时,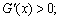 当
当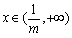 时,
时,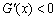 .
.
因此函数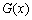 在
在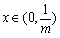 是增函数,在
是增函数,在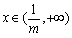 是减函数.
是减函数. 
故函数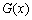 的最大值为
的最大值为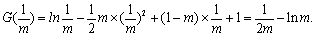 …………10分
…………10分
令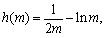 因为
因为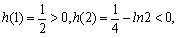
又因为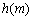 在
在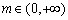 上是减函数,所以当
上是减函数,所以当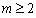 时,
时,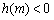 .
.
所以整数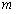 的最小值为2. ……………12分
的最小值为2. ……………12分
方法二:⑵由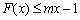 恒成立,得
恒成立,得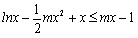 在
在 上恒成立.
上恒成立.
问题等价于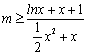 在
在 上恒成立.
上恒成立.
令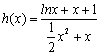 ,只要
,只要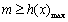 . ……………………6分
. ……………………6分
因为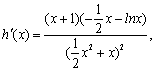 令
令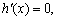 得
得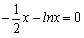 .
.
设 ,因为
,因为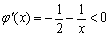 ,所以
,所以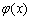 在
在 上单调递减,………………8分
上单调递减,………………8分
不妨设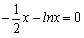 的根为
的根为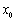 .当
.当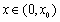 时,
时,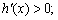 当
当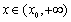 时,
时,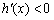 .
.
所以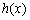 在
在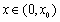 上是增函数;在
上是增函数;在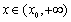 上是减函数.
上是减函数.
所以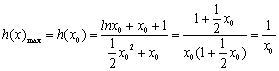 . …………………10分
. …………………10分
因为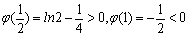

所以 此时
此时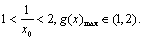 所以
所以 即整数
即整数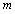 的最小值为2 …… 12分
的最小值为2 …… 12分

练习册系列答案
相关题目
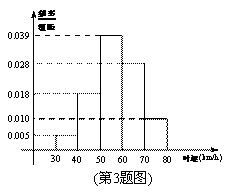
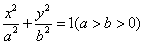 的左顶点为
的左顶点为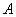 (-2,0),且过点
(-2,0),且过点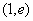 ,(e为椭圆的离心率);过
,(e为椭圆的离心率);过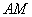 ,
,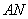 交椭圆于
交椭圆于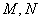 两点。
两点。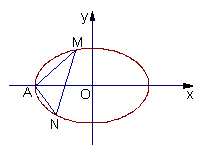 (1)求点椭圆的方程;
(1)求点椭圆的方程;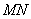 恒过
恒过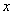 轴上的一个定点。
轴上的一个定点。  的值为二项式
的值为二项式 展开式的常数项,则输出的
展开式的常数项,则输出的 值是( )
值是( ) B.
B. C.
C. D.
D.

 中,
中, ,
, ,
, 是
是 的个位数字,
的个位数字, 是
是 的前
的前 项和,则
项和,则 .
. 的四个命题:
的四个命题: :
: ,
,
 ,
, 的共轭复数为
的共轭复数为 ,
, 的虚部为
的虚部为 ,其中真命题为
,其中真命题为 B.
B. C.
C. D.
D.
 在区间
在区间 上的导函数为
上的导函数为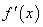 ,
, ,若在区间
,若在区间 恒成立,则称函数
恒成立,则称函数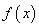 在区间
在区间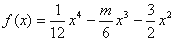 在
在 上为“凸函数”,则实数m的取值范围是
上为“凸函数”,则实数m的取值范围是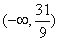 B.
B.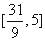 C.
C. D.
D.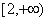
 +
+ =1,则x+y的最小值是( )
=1,则x+y的最小值是( )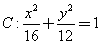 ,直线
,直线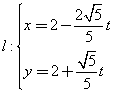 (
(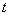 为参数)
为参数)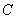 的参数方程,直线
的参数方程,直线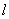 的普通方程;
的普通方程;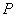 作与
作与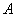 ,求
,求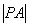 的最大值及此时P点的坐标。
的最大值及此时P点的坐标。