题目内容
在等差数列{an}中，已知公差d＝2，a2是a1与a4的等比中项．
(1)求数列{an}的通项公式；
(2)设bn＝
，记Tn＝－b1＋b2－b3＋b4－…＋(－1)nbn，求Tn.
解 (1)由题意知(a1＋d)2＝a1(a1＋3d)，
即(a1＋2)2＝a1(a1＋6)，解得a1＝2，
所以数列{an}的通项公式为an＝2n.
(2)由题意知bn＝
＝n(n＋1)，
所以Tn＝－1×2＋2×3－3×4＋…＋(－1)nn·(n＋1)．
因为bn＋1－bn＝2(n＋1)，可得当n为偶数时，
Tn＝(－b1＋b2)＋(－b3＋b4)＋…＋(－bn－1＋bn)
练习册系列答案
相关题目
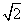，过点A作BC的垂线，垂足为A1；过点A1作AC的垂线，垂足为A2；过点A2作A1C的垂线，垂足为A3；…，依此类推，设BA＝a1，AA1＝a2，A1A2＝a3，…，A5A6＝a7，则a7＝________.
等于( )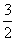
an＋n－3.
＋
＋…＋
≥
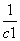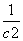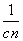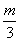都成立？若存在，求出m的值；若不存在，请说明理由．
＋2
，b＝2＋
，则a，b的大小关系为________．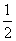
×底×高；(3)三角形的中位线平行于第三边且等于第三边的