题目内容
已知{an}是等差数列,公差为d,首项a1=3,前n项和为Sn.令cn=(-1)nSn(n∈N*),{cn}的前20项和T20=330.数列{bn}满足bn=2(a-2)dn-2+2n-1,a∈R.
(1)求数列{an}的通项公式;
(2)若bn+1≤bn,n∈N*,求a的取值范围.
解 (1)设等差数列{an}的公差为d,
因为cn=(-1)nSn,
所以T20=-S1+S2-S3+S4+…+S20=330,则a2+a4+a6+…+a20=330,
即10(3+d)+ ×2d=330,解得d=3,
×2d=330,解得d=3,
所以an=3+3(n-1)=3n.
(2)由(1)知bn=2(a-2)3n-2+2n-1,
bn+1-bn=2(a-2)3n-1+2n-[2(a-2)3n-2+2n-1]=4(a-2)3n-2+2n-1
=
由bn+1≤bn⇔(a-2)+
 n-2≤0
n-2≤0
⇔a≤2-
 n-2,
n-2,
因为2-
 n-2随着n的增大而增大,
n-2随着n的增大而增大,
所以n=1时,2-
 n-2取得最小值
n-2取得最小值 .
.
所以a≤ .
.

练习册系列答案
相关题目
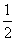 ,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
,a6+a7=3.则满足a1+a2+…+an>a1a2…an的最大正整数n的值为________.
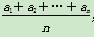 ,n∈N*,则数列{bn}的前n项和是( )
,n∈N*,则数列{bn}的前n项和是( ) ,记Tn=-b1+b2-b3+b4-…+(-1)nbn,求Tn.
,记Tn=-b1+b2-b3+b4-…+(-1)nbn,求Tn.