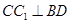题目内容
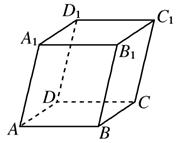
如图，平行六面体ABCD-A1B1C1D1中| A1C |
| AB |
| BC |
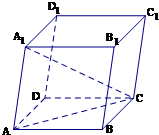
| CC1 |
分析：利用空间向量的平行六面体法则可得
=
+
+
，再利用向量共线及相等、平面向量的基本定理即可得出．
| A1C |
| A1B1 |
| A1D1 |
| A1A |
解答：解：在平行六面体ABCD-A1B1C1D1中可得：
=
，
=
，
=
．
∴
=
+
+
=
+
+
=x
+2y
+3z
，则x=1，2y=1，-3z=1，解得x=1，y=
，z=-
．
∴x+y+z=1+
-
=
．
故选C．
| A1B1 |
| AB |
| A1D1 |
| BC |
| A1A |
| C1C |
∴
| A1C |
| A1B1 |
| A1D1 |
| A1A |
| AB |
| BC |
| C1C |
| AB |
| BC |
| CC1 |
| 1 |
| 2 |
| 1 |
| 3 |
∴x+y+z=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 7 |
| 6 |
故选C．
点评：熟练掌握空间向量的平行六面体法则和向量共线定理、平面向量的基本定理即可得出．
练习册系列答案
相关题目
如图，平行六面体ANCD-EFGH中，棱AB，AD，AE的长分别为3，4，5，∠EAD=∠EAB=∠DAB=120°，则AG的长为
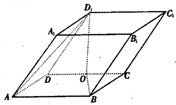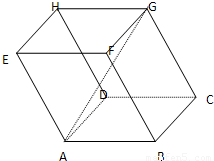
如图，平行六面体ABCD-A1B1C1D1中，AB=2，AD=1，底面ABCD是矩形，顶点D1在底面ABCD上的射影O恰好是CD的中点．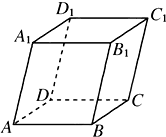
如图，平行六面体ABCD-A1B1C1D1中，∠BAD=∠BAA1=∠DAA1=60°，
