题目内容
1．双曲线x2-y2=2的右准线方程为x=1．分析 先把双曲线方程化为标准形式，再利用双曲线的简单性质直接求解．
解答 解：把x2-y2=2化为标准形式，得：$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}=1$
∴a=b=$\sqrt{2}$，c=2，
∴其右准线方程为：x=1．
故答案为：x=1．
点评 本题以双曲线方程为载体，考查双曲线的标准方程，考查双曲线的几何性质，属于基础题．
练习册系列答案
相关题目
9．一椭圆的中心在原点，焦点F1、F2在x轴上，点P是椭圆上一点，线段PF1与y轴的交点M是该线段的中点，若|PF2|=|MF2|，则椭圆的离心率等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
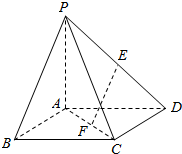如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，侧棱PA⊥底面ABCD，PA=AD=1，E、F分别为PD、AC上的动点，且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ（0＜λ＜1）．
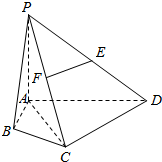如图，在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2AB=2
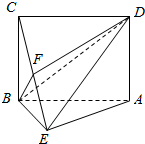已知如图：四边形ABCD是矩形，BC⊥平面ABE，且AE=EB=BC=2，点F为CE上一点，且BF⊥平面ACE．