题目内容
16.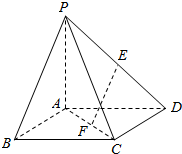 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).(Ⅰ)当λ=$\frac{1}{2}$时,求证:AD⊥EF;
(Ⅱ)求三棱锥E-FAD的体积的最大值.
分析 (Ⅰ)当λ=$\frac{1}{2}$时,E、F分别为PD、AC的中点,取AD中点H,连接EH、FH,则:EH∥PA,证明AD⊥面EFH.由此能证明AD⊥EF;
(Ⅱ)在平面PAD内作EH⊥AD于H,则EH⊥平面ADC,EH∥PAEH=λPA=λ.S△FAD=$\frac{1-λ}{2}$,由此能求出三棱锥E-FAD体积最大值.
解答 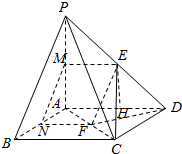 (Ⅰ)证明:当λ=$\frac{1}{2}$时,E、F分别为PD、AC的中点,
(Ⅰ)证明:当λ=$\frac{1}{2}$时,E、F分别为PD、AC的中点,
取AD中点H,连接EH、FH,则:EH∥PA
而PA⊥底面ABCD,
∴EH⊥平面ADC,且AD?面ABCD
∴EH⊥AD…?…(2分)
又FH∥CD且ABCD为正方形
∴FH⊥AD …?…(4分)
∵EH∩FH=H,
∴AD⊥面EFH
而EF?面EFH
∴AD⊥EF; …(6分)
(Ⅱ)解:在平面PAD内作EH⊥AD于H,
因为侧棱PA⊥底面ABCD,
所以平面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,
所以EH⊥平面ADC,所以EH∥PA.
因为$\frac{DE}{DP}$=λ(0<λ<1),所以$\frac{EH}{PA}$=λ,EH=λPA=λ.
∵$\frac{{S}_{△FAD}}{{S}_{△ADC}}$=$\frac{AF}{AC}$=1-λ,∴S△FAD=$\frac{1-λ}{2}$ …(10分)
∴VE-FAD=$\frac{1}{3}λ•\frac{1-λ}{2}$=$\frac{λ-{λ}^{2}}{6}$(0<λ<1)
∴三棱锥E-FAD的体积的最大值为$\frac{1}{24}$.…(13分)
点评 本题考查直线与平面垂直的证明,考查三棱锥的体积的最大值的求法,考查学生分析解决问题的能力,注意空间思维能力的培养.

 目标测试系列答案
目标测试系列答案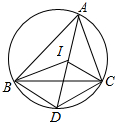 已知:如图,点I是△ABC的内心,延长AI交△ABC的外接圆于点D,求证:点D是△BCI的外心.
已知:如图,点I是△ABC的内心,延长AI交△ABC的外接圆于点D,求证:点D是△BCI的外心.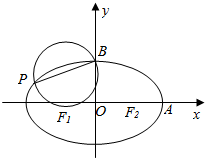 设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.
设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.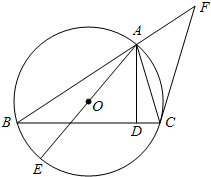 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.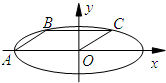 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.