题目内容
已知(2-3a)-
<(2a+1)-
,则实数a的取值范围为 .
| 1 |
| 2 |
| 1 |
| 2 |
考点:指、对数不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:运用幂函数y=x-
在(0,+∞)上递减,得到2-3a>0,且2a+1>0,且2-3a>2a+1,解出它们,即可得到a的取值范围.
| 1 |
| 2 |
解答:
解:由于2-3a>0,即有a<
,
再由不等式可知,2a+1>0,即a>-
,
即有-
<a<
,
再由(2-3a)-
<(2a+1)-
,
可得,2-3a>2a+1,解得,a<
.
综上可得,-
<a<
.
故答案为:(-
,
).
| 2 |
| 3 |
再由不等式可知,2a+1>0,即a>-
| 1 |
| 2 |
即有-
| 1 |
| 2 |
| 2 |
| 3 |
再由(2-3a)-
| 1 |
| 2 |
| 1 |
| 2 |
可得,2-3a>2a+1,解得,a<
| 1 |
| 5 |
综上可得,-
| 1 |
| 2 |
| 1 |
| 5 |
故答案为:(-
| 1 |
| 2 |
| 1 |
| 5 |
点评:本题考查幂函数的性质和运用:解不等式,考查运算能力,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
椭圆
+
=1的焦点坐标是( )
| x2 |
| 8 |
| y2 |
| 12 |
| A、(±4,0) |
| B、(0,±1) |
| C、(±3,0) |
| D、(0,±2) |
三角形三边长为a,b,c,且满足关系式(a+b+c)(a+b-c)=3ab,则c边的对角等于( )
| A、15° | B、45° |
| C、60° | D、120° |
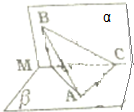 在直二面角α-MN-β中,等腰直角△ABC的斜边BC?α,一直角边AC?β,BC与β所成角的正弦值为
在直二面角α-MN-β中,等腰直角△ABC的斜边BC?α,一直角边AC?β,BC与β所成角的正弦值为
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
