题目内容
已知圆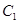 的参数方程为
的参数方程为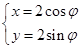 (
(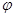 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆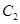 的极坐标方程为
的极坐标方程为 .
.
(1)将圆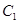 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆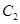 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆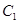 ,
,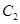 是否相交?若相交,请求出公共弦长,若不相交,请说明理由.
是否相交?若相交,请求出公共弦长,若不相交,请说明理由.
(1) ,
, ;(2)相交,两圆的相交弦长为
;(2)相交,两圆的相交弦长为 .
.
解析试题分析:本题考查坐标系与参数方程、极坐标与直角坐标方程的互化,考查学生的转化能力和计算能力.第一问,利用互化公式将参数方程化为普通方程,将极坐标方程化为直角坐标方程;第二问,通过数形结合,利用几何性质求相交弦长.
试题解析:(1)由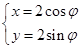 (
(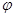 为参数),得
为参数),得 ,
,
由 ,得
,得 ,
,
即 ,整理得,
,整理得, . 5分
. 5分
(2)由于圆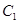 表示圆心为原点,半径为2的圆,圆
表示圆心为原点,半径为2的圆,圆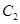 表示圆心为
表示圆心为 ,半径为2的圆,
,半径为2的圆,
又圆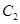 的圆心
的圆心 在圆
在圆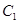 上,由几何性质易知,两圆的相交弦长为
上,由几何性质易知,两圆的相交弦长为 . 10分
. 10分
考点:1.参数方程与普通方程的互化;2.极坐标方程与直角坐标方程的互化;3.相交弦问题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( ).
| A.a1>a2 | B.a1<a2 |
| C.a1=a2 | D.a1,a2的大小与m的值有关 |
 中,已知直线
中,已知直线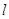 的参数方程
的参数方程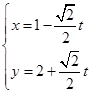 (
(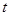 为参数),直线
为参数),直线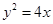 相交于
相交于 两点,求线段
两点,求线段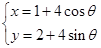 (
( 为参数),直线
为参数),直线 经过定点P(3,5),倾斜角为
经过定点P(3,5),倾斜角为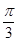 (1)写出直线
(1)写出直线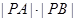 的值
的值 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为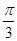 .
. (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ. ,求α的值.
,求α的值.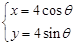 (
(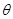 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角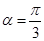 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;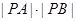 的值。
的值。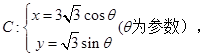 直线
直线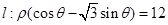
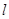 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程; 中,曲线
中,曲线 的参数方程为
的参数方程为 ,
, 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
. 时,曲线
时,曲线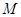 、
、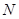 两点,求以线段
两点,求以线段 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.