题目内容
证明:若在(a,b)内f″(x)>0,则f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2),其中λ1+λ2=1.
考点:利用导数研究函数的单调性
专题:证明题,导数的综合应用
分析:由题意可判断f(x)是定义在闭区间[a,b]上凸函数,再由凸函数的定义证明.
解答:
证明:∵在(a,b)内f″(x)>0,
∴f(x)是定义在闭区间[a,b]上凸函数;
而根据上凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”;
故取x=x1,y=x2,λ=λ1,1-λ=1-λ1=λ2,
而任意正数λ1,λ2,λ1+λ2=1,x1、x2∈(a,b);
得不等式f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)对于任意的x1,x2∈(a,b)恒成立.
∴f(x)是定义在闭区间[a,b]上凸函数;
而根据上凸函数的定义“f(x)是定义在闭区间[a,b]上的函数,若任意x,y∈[a,b]和任意λ∈(0,1),有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)成立”;
故取x=x1,y=x2,λ=λ1,1-λ=1-λ1=λ2,
而任意正数λ1,λ2,λ1+λ2=1,x1、x2∈(a,b);
得不等式f(λ1x1+λ2x2)≤λ1f(x1)+λ2f(x2)对于任意的x1,x2∈(a,b)恒成立.
点评:本题考查了凸函数的判断与凸函数的定义的应用及判断,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=5x-3sinx,x∈(-2,2),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A、(1,
| ||
| B、(1,3) | ||
| C、(-∞,-2)∪(1,+∞) | ||
| D、(-2,1) |
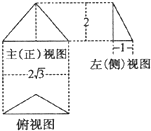 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为