题目内容
(本小题满分13分)设椭圆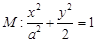
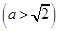 的右焦点为
的右焦点为 ,直线
,直线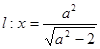 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点).
(1)求椭圆 的方程;
的方程;
(2)设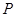 是椭圆
是椭圆 上的任意一点,
上的任意一点,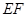 为圆
为圆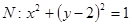 的任意一条直径(
的任意一条直径(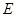 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.
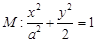
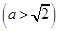 的右焦点为
的右焦点为 ,直线
,直线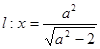 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点).(1)求椭圆
 的方程;
的方程;(2)设
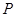 是椭圆
是椭圆 上的任意一点,
上的任意一点,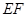 为圆
为圆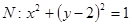 的任意一条直径(
的任意一条直径(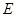 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.(1)椭圆 的方程为
的方程为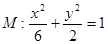 . (2)
. (2) 的最大值为11.
的最大值为11.
 的方程为
的方程为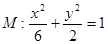 . (2)
. (2) 的最大值为11.
的最大值为11. (1)由题设知,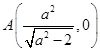 ,
,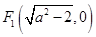 ,由
,由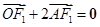 ,得
,得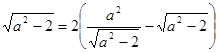 ,从而得到关于a的方程,求出a值.
,从而得到关于a的方程,求出a值.
(2)设圆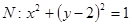 的圆心为
的圆心为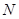 ,则
,则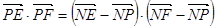

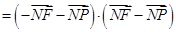
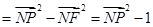 ,
,
从而把 的最大值转化为求
的最大值转化为求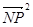 的最大值,再利用两点间的距离公式再借助P在椭圆上,可以把
的最大值,再利用两点间的距离公式再借助P在椭圆上,可以把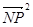 转化为关于P的横坐标x的函数问题来解决.
转化为关于P的横坐标x的函数问题来解决.
(1)由题设知,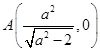 ,
,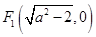 ,………………………1分
,………………………1分
由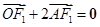 ,得
,得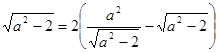 .………………3分
.………………3分
解得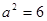 .所以椭圆
.所以椭圆 的方程为
的方程为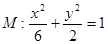 .…………………4分
.…………………4分
(2)方法1:设圆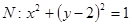 的圆心为
的圆心为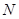 ,
,
则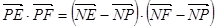 ……………………6分
……………………6分

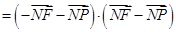 ……K…………………………7分
……K…………………………7分
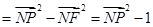 .………………………………………8分
.………………………………………8分
从而求 的最大值转化为求
的最大值转化为求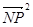 的最大值.………………………9分
的最大值.………………………9分
因为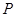 是椭圆
是椭圆 上的任意一点,设
上的任意一点,设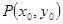 ,……………………………10分
,……………………………10分
所以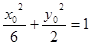 ,即
,即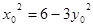 .…………………………11分
.…………………………11分
因为点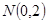 ,所以
,所以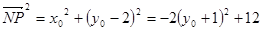 .……………12分
.……………12分
因为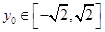 ,所以当
,所以当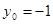 时,
时,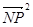 取得最大值12.……………13分
取得最大值12.……………13分
所以 的最大值为11.……………………………14分
的最大值为11.……………………………14分
方法2:设点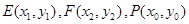 ,
,
因为 的中点坐标为
的中点坐标为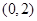 ,所以
,所以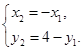 …………………………6分
…………………………6分
所以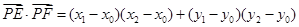 ……………………7分
……………………7分
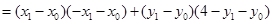
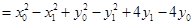
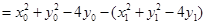 .……………………………9分
.……………………………9分
因为点 在圆
在圆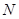 上,所以
上,所以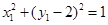 ,即
,即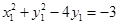 .…………10分
.…………10分
因为点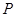 在椭圆
在椭圆 上,所以
上,所以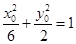 ,即
,即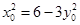 .………………11分
.………………11分
所以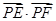
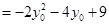
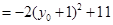 .……………………………12分
.……………………………12分
因为 ,所以当
,所以当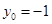 时,
时,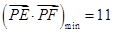 .…………………14分
.…………………14分
方法3:①若直线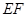 的斜率存在,设
的斜率存在,设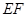 的方程为
的方程为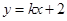 ,……………6分
,……………6分
由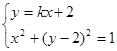 ,解得
,解得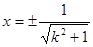 .………………………7分
.………………………7分
因为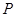 是椭圆
是椭圆 上的任一点,设点
上的任一点,设点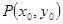 ,
,
所以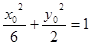 ,即
,即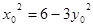 .…………………8分
.…………………8分
所以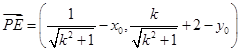 ………9分
………9分
所以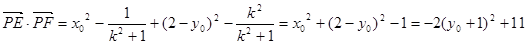 .
.
………10分
因为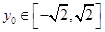 ,所以当
,所以当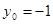 时,
时, 取得最大值11.……………11分
取得最大值11.……………11分
②若直线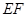 的斜率不存在,此时
的斜率不存在,此时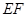 的方程为
的方程为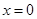 ,
,
由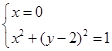 ,解得
,解得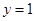 或
或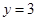 .
.
不妨设,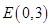 ,
,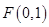 .……………………5u…………………12分
.……………………5u…………………12分
因为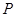 是椭圆
是椭圆 上的任一点,设点
上的任一点,设点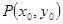 ,
,
所以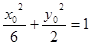 ,即
,即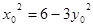 .
.
所以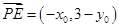 ,
,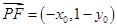 .
.
所以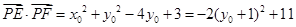 .
.
因为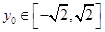 ,所以当
,所以当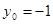 时,
时, 取得最大值11.………13分
取得最大值11.………13分
综上可知, 的最大值为11.…………………………………14分
的最大值为11.…………………………………14分
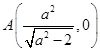 ,
,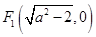 ,由
,由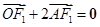 ,得
,得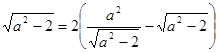 ,从而得到关于a的方程,求出a值.
,从而得到关于a的方程,求出a值.(2)设圆
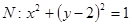 的圆心为
的圆心为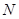 ,则
,则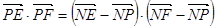

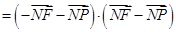
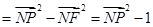 ,
,从而把
 的最大值转化为求
的最大值转化为求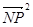 的最大值,再利用两点间的距离公式再借助P在椭圆上,可以把
的最大值,再利用两点间的距离公式再借助P在椭圆上,可以把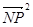 转化为关于P的横坐标x的函数问题来解决.
转化为关于P的横坐标x的函数问题来解决.(1)由题设知,
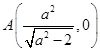 ,
,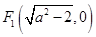 ,………………………1分
,………………………1分由
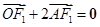 ,得
,得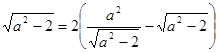 .………………3分
.………………3分解得
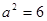 .所以椭圆
.所以椭圆 的方程为
的方程为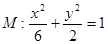 .…………………4分
.…………………4分(2)方法1:设圆
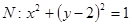 的圆心为
的圆心为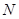 ,
,则
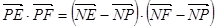 ……………………6分
……………………6分
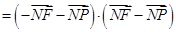 ……K…………………………7分
……K…………………………7分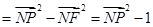 .………………………………………8分
.………………………………………8分从而求
 的最大值转化为求
的最大值转化为求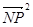 的最大值.………………………9分
的最大值.………………………9分因为
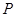 是椭圆
是椭圆 上的任意一点,设
上的任意一点,设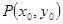 ,……………………………10分
,……………………………10分所以
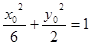 ,即
,即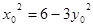 .…………………………11分
.…………………………11分因为点
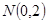 ,所以
,所以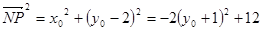 .……………12分
.……………12分因为
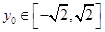 ,所以当
,所以当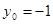 时,
时,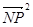 取得最大值12.……………13分
取得最大值12.……………13分所以
 的最大值为11.……………………………14分
的最大值为11.……………………………14分方法2:设点
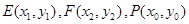 ,
,因为
 的中点坐标为
的中点坐标为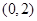 ,所以
,所以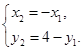 …………………………6分
…………………………6分所以
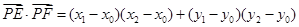 ……………………7分
……………………7分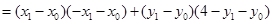
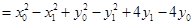
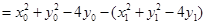 .……………………………9分
.……………………………9分因为点
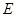 在圆
在圆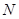 上,所以
上,所以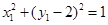 ,即
,即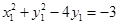 .…………10分
.…………10分因为点
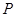 在椭圆
在椭圆 上,所以
上,所以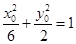 ,即
,即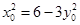 .………………11分
.………………11分所以
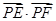
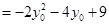
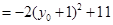 .……………………………12分
.……………………………12分因为
 ,所以当
,所以当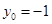 时,
时,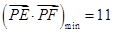 .…………………14分
.…………………14分方法3:①若直线
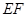 的斜率存在,设
的斜率存在,设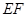 的方程为
的方程为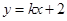 ,……………6分
,……………6分由
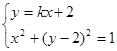 ,解得
,解得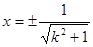 .………………………7分
.………………………7分因为
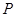 是椭圆
是椭圆 上的任一点,设点
上的任一点,设点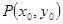 ,
,所以
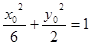 ,即
,即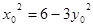 .…………………8分
.…………………8分所以
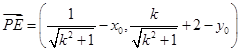 ………9分
………9分所以
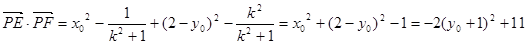 .
.………10分
因为
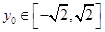 ,所以当
,所以当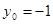 时,
时, 取得最大值11.……………11分
取得最大值11.……………11分②若直线
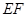 的斜率不存在,此时
的斜率不存在,此时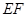 的方程为
的方程为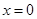 ,
, 由
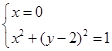 ,解得
,解得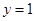 或
或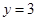 .
.不妨设,
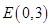 ,
,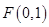 .……………………5u…………………12分
.……………………5u…………………12分因为
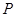 是椭圆
是椭圆 上的任一点,设点
上的任一点,设点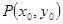 ,
,所以
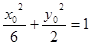 ,即
,即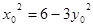 .
.所以
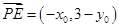 ,
,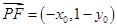 .
.所以
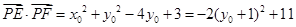 .
. 因为
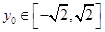 ,所以当
,所以当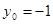 时,
时, 取得最大值11.………13分
取得最大值11.………13分综上可知,
 的最大值为11.…………………………………14分
的最大值为11.…………………………………14分
练习册系列答案
相关题目
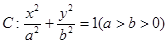 过点
过点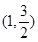 ,且离心率e=
,且离心率e=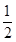 .
.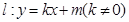 与椭圆交于不同的两点
与椭圆交于不同的两点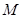 、
、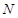 ,且线段
,且线段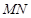 的垂直平分线过定点
的垂直平分线过定点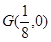 ,求
,求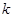 的取值范围。
的取值范围。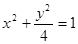 的离心率为( )
的离心率为( )


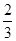
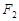 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,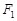 的直线MF1是圆
的直线MF1是圆 ,焦点
,焦点 ,右准线
,右准线 与
与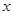 轴相交于点
轴相交于点 ,且
,且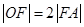 ,过点
,过点 .
. ,求直线
,求直线 的方程.
的方程. ,离心率
,离心率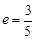 ,焦点在
,焦点在 轴上的椭圆标准方程是 ( )
轴上的椭圆标准方程是 ( )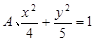
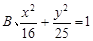
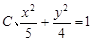
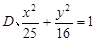
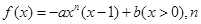 为正整数,
为正整数,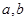 为常数.曲线
为常数.曲线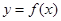 在点
在点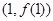 处的切线方程为
处的切线方程为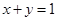 .
.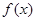 的最大值;
的最大值;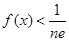 .
. 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点, 的最小值为2,则其离心率为( )
的最小值为2,则其离心率为( )

 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________