题目内容
标准方程下的椭圆的短轴长为 ,焦点
,焦点 ,右准线
,右准线 与
与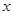 轴相交于点
轴相交于点 ,且
,且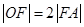 ,过点
,过点 的直线和椭圆相交于点
的直线和椭圆相交于点 .
.
(1)求椭圆的方程和离心率;
(2)若 ,求直线
,求直线 的方程.
的方程.
 ,焦点
,焦点 ,右准线
,右准线 与
与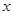 轴相交于点
轴相交于点 ,且
,且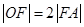 ,过点
,过点 的直线和椭圆相交于点
的直线和椭圆相交于点 .
.(1)求椭圆的方程和离心率;
(2)若
 ,求直线
,求直线 的方程.
的方程. (1) ,
,  ;(2)
;(2) 。
。
 ,
,  ;(2)
;(2) 。
。本试题主要是考查了直线与圆的位置关系综合运用。
(1)由题意,设该椭圆方程为 ,根据条件有
,根据条件有
 得到椭圆的方程。
得到椭圆的方程。
(2)设直线 的方程为
的方程为 ,联立椭圆方程有
,联立椭圆方程有

和向量的数量积为零得到结论。
解:(1)由题意,设该椭圆方程为 ,根据条件有
,根据条件有
 ,所以椭圆的方程为
,所以椭圆的方程为 ,离心率
,离心率
(2)设直线 的方程为
的方程为 ,联立椭圆方程有
,联立椭圆方程有

又 ,即
,即 ,
,
而
于是有 ,
,
由(1)(2)(3)得, ,经检验符合
,经检验符合
所以直线
(1)由题意,设该椭圆方程为
 ,根据条件有
,根据条件有 得到椭圆的方程。
得到椭圆的方程。(2)设直线
 的方程为
的方程为 ,联立椭圆方程有
,联立椭圆方程有
和向量的数量积为零得到结论。
解:(1)由题意,设该椭圆方程为
 ,根据条件有
,根据条件有 ,所以椭圆的方程为
,所以椭圆的方程为 ,离心率
,离心率
(2)设直线
 的方程为
的方程为 ,联立椭圆方程有
,联立椭圆方程有
又
 ,即
,即 ,
,而

于是有
 ,
,由(1)(2)(3)得,
 ,经检验符合
,经检验符合所以直线


练习册系列答案
相关题目
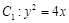 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆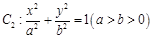 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为 在第一象限的交点为
在第一象限的交点为 为坐标原点,且
为坐标原点,且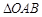 的面积为
的面积为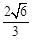
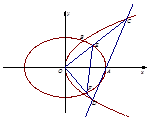
 的标准方程;
的标准方程;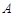 作直线
作直线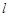 交
交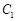 于
于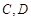 两点,射线
两点,射线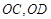 分别交
分别交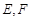 两点.
两点. 点在以
点在以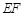 为直径的圆的内部;
为直径的圆的内部;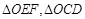 的面积分别为
的面积分别为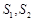 ,问是否存在直线
,问是否存在直线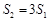 ?请说明理由.
?请说明理由.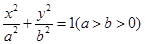 ,
,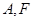 是其左顶点和左焦点,
是其左顶点和左焦点,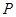 是圆
是圆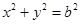 上的动点,若
上的动点,若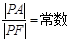 ,则此椭圆的离心率是
,则此椭圆的离心率是 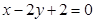 经过椭圆
经过椭圆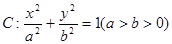 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆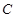 的右顶点为
的右顶点为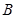 ,点
,点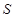 是椭圆
是椭圆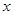 轴上方的动点,直线
轴上方的动点,直线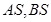 与直线
与直线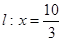 分别交于
分别交于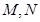 两点。
两点。
 的长度的最小值;
的长度的最小值; ,使得
,使得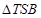 的面积为
的面积为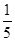 ?若存在,确定点
?若存在,确定点 ,点
,点 是圆内异于
是圆内异于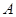 是圆周上一点.把纸片折叠使点
是圆周上一点.把纸片折叠使点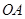 交于
交于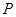 点.当点
点.当点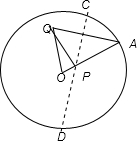
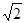 ,焦点到相应准线的
,焦点到相应准线的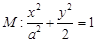
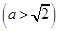 的右焦点为
的右焦点为 ,直线
,直线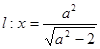 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点). 的方程;
的方程;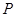 是椭圆
是椭圆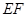 为圆
为圆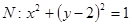 的任意一条直径(
的任意一条直径(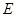 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.


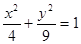 于A、B两点,且M为AB的中点,则直线l方程为 .
于A、B两点,且M为AB的中点,则直线l方程为 .