题目内容
设椭圆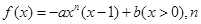 为正整数,
为正整数,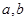 为常数.曲线
为常数.曲线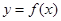 在点
在点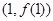 处的切线方程为
处的切线方程为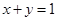 .
.
(Ⅰ)求函数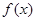 的最大值;
的最大值;
(Ⅱ)证明: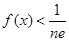 .
.
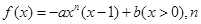 为正整数,
为正整数,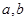 为常数.曲线
为常数.曲线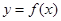 在点
在点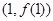 处的切线方程为
处的切线方程为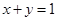 .
.(Ⅰ)求函数
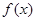 的最大值;
的最大值;(Ⅱ)证明:
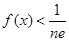 .
.(Ⅰ)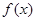 在
在 上最大值为
上最大值为
(Ⅱ)证明略
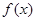 在
在 上最大值为
上最大值为
(Ⅱ)证明略
本试题主要是考查了导数在研究函数中的运用。
(1)第一问中利用导数的几何意义求解得到。
(2)利用导数的符号判定函数单调性,然后求解函数的极值和最值问题。
(3)欲证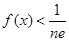 成立,只需证:
成立,只需证:
即证: 即
即
构造函数证明不等式。
(1)第一问中利用导数的几何意义求解得到。
(2)利用导数的符号判定函数单调性,然后求解函数的极值和最值问题。
(3)欲证
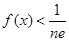 成立,只需证:
成立,只需证:
即证:
 即
即
构造函数证明不等式。

练习册系列答案
相关题目
 与椭圆
与椭圆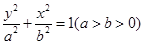 交于
交于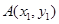 ,
,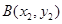 两点,已知
两点,已知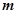
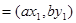 ,
,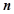
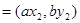 ,若
,若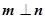 且椭圆的离心率
且椭圆的离心率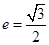 ,又椭圆经过点
,又椭圆经过点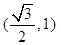 ,
, 为坐标原点.
为坐标原点. (
(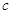 为半焦距),求直线
为半焦距),求直线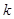 的值;
的值;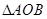 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.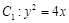 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆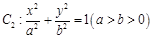 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为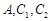 在第一象限的交点为
在第一象限的交点为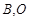 为坐标原点,且
为坐标原点,且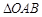 的面积为
的面积为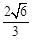
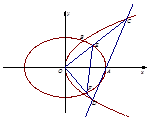
 的标准方程;
的标准方程; 作直线
作直线 交
交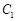 于
于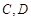 两点,射线
两点,射线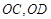 分别交
分别交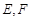 两点.
两点.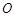 点在以
点在以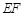 为直径的圆的内部;
为直径的圆的内部;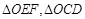 的面积分别为
的面积分别为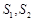 ,问是否存在直线
,问是否存在直线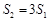 ?请说明理由.
?请说明理由.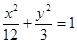 的左焦点为
的左焦点为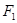 , 点
, 点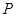 在椭圆上, 如果线段
在椭圆上, 如果线段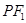 的中点
的中点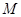 在
在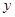 轴的
轴的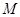 的坐标是 .
的坐标是 .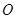 ,点
,点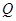 是圆内异于
是圆内异于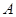 是圆周上一点.把纸片折叠使点
是圆周上一点.把纸片折叠使点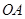 交于
交于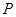 点.当点
点.当点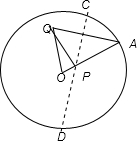
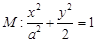
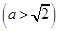 的右焦点为
的右焦点为 ,直线
,直线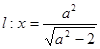 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点). 的方程;
的方程;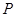 是椭圆
是椭圆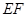 为圆
为圆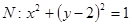 的任意一条直径(
的任意一条直径(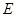 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.


 在
在 轴的非负半轴上,点
轴的非负半轴上,点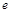 ;
; 为焦点
为焦点 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使 (
(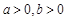 )的一条渐近线方程为
)的一条渐近线方程为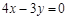 ,则该双曲
,则该双曲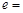 _________.
_________.