题目内容
20.已知{an}是等差数列,a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}是等比数列.(1)求数列{an}和{bn}的通项公式;
(2)设cn=bncosnπ,求数列{cn}的前n项和Sn,并判断是否存在正整数m,使得Sm=2016?若存在,求出m的值;若不存在,说明理由.
分析 (1)可求得d=$\frac{{a}_{4}-{a}_{1}}{4-1}$=3,{bn-an}是等比数列,公比q=2,从而求数列{an}和{bn}的通项公式;
(2)化简cn=bncosnπ=(3n+2n-1)cosnπ,从而分类讨论以确定数列{cn}的前n项和Sn,可求得Sn=$\left\{\begin{array}{l}{-(\frac{3}{2}n+\frac{3}{2}+\frac{1}{3}({2}^{n}+1)),n为奇数}\\{\frac{3}{2}n+\frac{1}{3}({2}^{n}-1),n为偶数}\end{array}\right.$,从而讨论即可.
解答 解:(1)∵{an}是等差数列,a1=3,a4=12,
∴d=$\frac{{a}_{4}-{a}_{1}}{4-1}$=3,
∴an=3n,
∵{bn-an}是等比数列,且b1-a1=4-3=1,b4-a4=20-12=8,
∴q=2,
∴bn-an=1•2n-1,
∴bn=3n+2n-1;
(2)cn=bncosnπ=(3n+2n-1)cosnπ,
故①当n为奇数时,
Sn=-(3+1)+(6+2)-(9+4)+…+(3(n-1)+2n-2)-(3n+2n-1)
=(-3+6-9+…+3(n-1))-3n+(-1+2-4+…-2n-1)
=3×$\frac{n-1}{2}$-3n+$\frac{1}{3}$[(-2)n-1]
=-$\frac{3}{2}$(n+1)+$\frac{1}{3}$[(-2)n-1]
=-[$\frac{3}{2}$(n+1)+$\frac{1}{3}$(2n+1)],
②当n为偶数时,
Sn=-(3+1)+(6+2)-(9+4)+…-(3(n-1)+2n-2)+(3n+2n-1)
=(-3+6-9+…-3(n-1)+3n)+(-1+2-4+…+2n-1)
=3×$\frac{n}{2}$+$\frac{1}{3}$[(-2)n-1]
=$\frac{3}{2}$n+$\frac{1}{3}$(2n-1),
综上所述,
Sn=$\left\{\begin{array}{l}{-(\frac{3}{2}n+\frac{3}{2}+\frac{1}{3}({2}^{n}+1)),n为奇数}\\{\frac{3}{2}n+\frac{1}{3}({2}^{n}-1),n为偶数}\end{array}\right.$,
若Sm=2016,故m一定是偶数,
故$\frac{3}{2}$m+$\frac{1}{3}$(2m-1)=2016,
故$\frac{1}{3}$(2m-1)=2016-$\frac{3}{2}$m,
而$\frac{1}{3}$(214-1)>2016,$\frac{1}{3}$(212-1)<2016-$\frac{3}{2}$×12,
故m值不存在.
点评 本题考查了等差数列与等比数列的应用,同时考查了数列前n项和的求法及分类讨论的思想应用.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{8}$π | B. | $\frac{1}{2}$π | C. | $\frac{3}{4}$π | D. | $\frac{3}{8}$π |
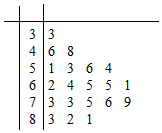 某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意(1)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“満意”与“否”与性别有有关?
附:
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(3)从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为ξ,求ξ的分布列与数学期望.
| A. | (-$\frac{1}{3}$,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |
| A. | 1,$\frac{π}{2}$ | B. | 1,-$\frac{π}{2}$ | C. | 3,$\frac{π}{6}$ | D. | 3,-$\frac{π}{6}$ |