题目内容
10个相同的小球装进编号为1、2、3的盒子内，无多余的小球且每个盒子内小球的个数不小于盒子的编号数，那么共有（ ）种装法．
| A、12 | B、13 | C、14 | D、15 |
考点：计数原理的应用
专题：应用题,排列组合
分析：根据题意，要求符合题意的放法，分两步，①先在编号为2、3的三个盒子中分别放入1、2个小球，编号为1的盒子里不放；②再将剩下的7个小球放入3个盒子里，每个盒子里至少一个；进而使用隔板法分析可得答案．
解答：
解：根据题意，先在编号为2、3的三个盒子中分别放入1、2个小球，编号为1的盒子里不放；再将剩下的7个小球放入3个盒子里，每个盒子里至少一个，分析可得，共C62=15种放法，即可得符合题目要求的放法共15种，
故选：D．
故选：D．
点评：本题考查组合的运用，是一道典型的题目，注意解题的特殊方法．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与直线y=b （0＜b＜A）的三个相邻交点的横坐标分别是2，4，8，则f（x）的单调递增区间是（ ）
| A、[6kπ，6kπ+3]，k∈Z |
| B、[6k-3，6k]，k∈Z |
| C、[6k，6k+3]，k∈Z |
| D、无法确定 |
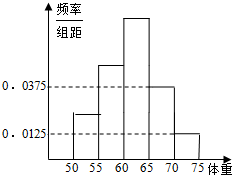为了了解高三学生的身体状况．抽取了部分男生的体重，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则抽取的男生人数是（ ）| A、96 | B、32 | C、18 | D、48 |
sin
•cos（-
）+tan（-
）•tan
的值是（ ）
| 7π |
| 3 |
| 11π |
| 6 |
| 15π |
| 4 |
| 13π |
| 3 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|