题目内容
2.用秦九韶算法计算多项式f(x)=3x6+5x5+6x4+79x3-8x2+35x+12在x=-4时的值时,运算总次数为( )| A. | 11 | B. | 12 | C. | 26 | D. | 27 |
分析 把所给的多项式写成关于x的一次函数的形式,依次写出,得到最后结果,从里到外进行运算,结果有6次乘法运算,有6次加法运算,本题也可以不分解,直接从最高次项的次数直接得到结果.
解答 解:∵f(x)=3x6+5x5+6x4+79x3-8x2+35x+12
=12+35x-8x2+79x3+6x4+5x5+3x6
=((3x+5)x+6)x+79)x-8)x+35)x+12,
∴需要做6次加法运算,6次乘法运算,
∴需要做乘法和加法的次数共12次,
故选:B.
点评 本题考查秦九韶算法,考查在用秦九韶算法解题时一共会进行多少次加法和乘法运算,是一个基础题,解题时注意最后加还是不加常数项,可以直接看出结果.

练习册系列答案
相关题目
14.已知集合M={x|x2-6x+5<0,x∈Z},N={1,2,3,4,5},则M∩N=( )
| A. | {1,2,3,4} | B. | {2,3,4,5} | C. | {2,3,4} | D. | {1,2,4,5} |
15.若$\frac{1}{a}$>$\frac{1}{b}$>0,有四个不等式:①a3<b3;②loga+23>logb+13;③④$\sqrt{b}$-$\sqrt{a}$<$\sqrt{b-a}$;④a3+b3>2ab2,则下列组合中全部正确的为( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①④ |
7.从标有1、2、3、4的卡片中不放回地先后抽出两张卡片,则4号卡片“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到的概率”分别是( )
| A. | $\frac{1}{4},\frac{1}{4},\frac{1}{2}$ | B. | $\frac{1}{4},\frac{1}{4},\frac{1}{4}$ | C. | $\frac{1}{3},\frac{1}{3},\frac{1}{2}$ | D. | $\frac{1}{4},\frac{1}{3},\frac{1}{2}$ |
12.若复数z满足(1+i)z=2+i,则复数z的共轭复数$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
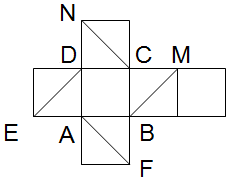 如图是正方体的平面展开图,则下列结论中正确的有(3)(4).
如图是正方体的平面展开图,则下列结论中正确的有(3)(4).