题目内容
10.已知等比数列{an}中,Sn=3n-1+r,求r.分析 由${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,先求出数列的前3项,再利用等比数列的性质能求出r的值.
解答 解:∵等比数列{an}中,Sn=3n-1+r,
∴a1=S1=31-1+r=1+r,
a2=S2-S1=3+r-(1+r)=2,
a3=S3-S2=(32+r)-(3+r)=6,
由等比数列的性质得:22=(1+r)×6,
解得r=-$\frac{1}{3}$.
点评 本题考查等比数列中实数值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知a∈R,则“|a-1|+|a|≤1”是“函数y=ax在R上为减函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2015}$的值的程序框图,其中判断框内应填入的是( )
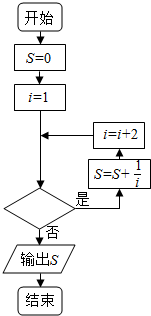

| A. | i≤2012 | B. | i≤2014 | C. | i≤2016 | D. | i≤2018 |