题目内容
3.若X是一个集合,т是一个以X的某些子集为元素的集合,且满足:①X属于т,∅属于т;②т中任意多个元素的并集属于т;③т中任意多个元素的交集属于т.则称т是集合X上的一个拓扑.已知函数f(x)=[x[x]],其中[x]表示不大于x的最大整数,当x∈(0,n],n∈N*时,函数f(x)值域为集合An,则集合A2上的含有4个元素的拓扑т的个数为9.分析 根据集合X上的拓扑的集合τ的定义,判断n的值,利用元素与集合的关系判断满足题意的集合A2上的含有4个元素的拓扑т的个数.
解答 解:函数f(x)=[x[x]],其中[x]表示不大于x的最大整数,当x∈(0,n],n∈N*时,函数f(x)值域为集合An,依题意,n=2,故0<x≤2,
①当0<x<1时,则[x]=0,∴f[x[x]]=0,
②当x=1时,[x]=1显然f(1)=1,
③当1<x<2时,[x]=1,∴f[x[x]]=[x]=1,
④当x=2时,f(2)=4,
∴A2={0,1,4},
∵т中含有4个元素,其中两个元素∅和A2,
∴A2={0,1,4}.其它两个元素为A,B,则$\left\{\begin{array}{l}A≠∅\\ A≠{A}_{2}\\ B≠∅\\ B≠{A}_{2}\\ A≠B\end{array}\right.$
由对称性,不妨设1≤|A|≤|B|≤2,其中|A|、|B|表示集合A中元素的个数,
∵$\left\{\begin{array}{l}A∩B∈т\\ A∪B∈т\end{array}\right.$,又|A|≤|B|,∴A∩B=∅或A,
若A∩B=∅,则A∪B只能等于A2,(若A∪B=B,则A⊆B,则A∩B=A=∅,矛盾)
则必有$\left\{\begin{array}{l}\left|A\right|=1\\ \left|B\right|=2\end{array}\right.$,∴(A,B)的个数?A的个数=3种.即$\left\{\begin{array}{l}A=\left\{0\right\}\\ B=\{1,4\}\end{array}\right.$或$\left\{\begin{array}{l}A=\left\{1\right\}\\ B=\{0,4\}\end{array}\right.$或$\left\{\begin{array}{l}A=\left\{4\right\}\\ B=\{0,1\}\end{array}\right.$
若A∩B=A?A⊆B此时满足A∪B=B,∵A≠B且1≤|A|且|B|≤2,∴$\left\{\begin{array}{l}\left|A\right|=1\\ \left|B\right|=2\end{array}\right.$,
∴B的选择共有${C}_{3}^{2}$=3种,则A的个数有${C}_{2}^{1}$种,
∴(A,B)的个数=2×3=6种.(这6种是$\left\{\begin{array}{l}A=\left\{0\right\}\\ B=\{0,1\}\end{array}\right.$,$\left\{\begin{array}{l}A=\left\{1\right\}\\ B=\{0,1\}\end{array}\right.$,$\left\{\begin{array}{l}A=\left\{0\right\}\\ B=\{0,4\}\end{array}\right.$,$\left\{\begin{array}{l}A=\left\{4\right\}\\ B=\{0,4\}\end{array}\right.$,$\left\{\begin{array}{l}A=\left\{1\right\}\\ B=\{1,4\}\end{array}\right.$,$\left\{\begin{array}{l}A=\left\{4\right\}\\ B=\{1,4\}\end{array}\right.$.
综上可知т的个数为9个.
故答案为:9.
点评 本题考查集合的关系,元素个数的判断,考查推理与证明,注意拓扑知识的应用,难度比较大.

| A. | -1 | B. | $\frac{π}{4}$ | C. | 1 | D. | 2 |
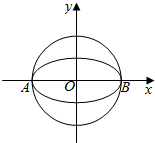 已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.