题目内容
18．做出函数（1）y=x2-2|x|+1（2）y=x2-|x+1|的简图，写出单调区间并求出值域．
分析 把绝对值函数化为分段函数，画出图象，观察图象即可．
解答 解：（（1）y=x2-2|x|+1=$\left\{\begin{array}{l}{{x}^{2}-2x+1，x≥0}\\{{x}^{2}+2x+1，x＜0}\end{array}\right.$图象如图所示：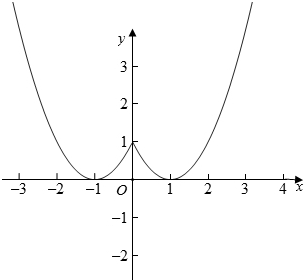
由图象可知，f（x）在（-∞，-1）和（0，1）上为减函数，在（-1，0）和（1，+∞）为增函数，其值域为[0，+∞）；
（2）y=x2-|x+1|=$\left\{\begin{array}{l}{{x}^{2}-x-1，x≥-1}\\{{x}^{2}+x+1，x＜-1}\end{array}\right.$的图象如图所示：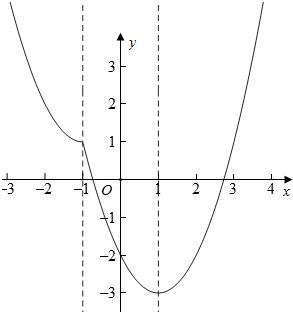
由图象可知，f（x）在（-∞，-1）和（-1，1）上为减函数，在（1，+∞）为增函数，其值域为[-3，+∞）；
点评 本题考查了绝对值函数的图象的画法和识别，属于基础题．
练习册系列答案
相关题目
9．函数y=1-2sinx的值域是（ ）
| A． | [-2，1] | B． | [-1，3] | C． | [0，1] | D． | [-2，3] |
10．
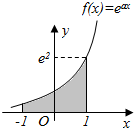已知函数f（x）=eax（a为常数）的图象如下图所示，则图中阴影部分（曲线y=f（x）与x轴，直线x=-1，x=1所围成的封闭图形）的面积是（ ）
已知函数f（x）=eax（a为常数）的图象如下图所示，则图中阴影部分（曲线y=f（x）与x轴，直线x=-1，x=1所围成的封闭图形）的面积是（ ）| A． | $\frac{{e}^{2}-{e}^{-2}}{2}$ | B． | $\frac{{e}^{2}+{e}^{-2}}{2}$ | C． | e2-e-2 | D． | e2+e-2 |
