题目内容
8．已知AC、BD为圆x2+y2=4的两条互相垂直的弦，AC与BD相交于点M$（1，\sqrt{2}）$，则四边形ABCD面积的最大值为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 设圆心到AC、BD的距离分别为d1、d2，则 d12+d22 =3，代入面积公式S=$\frac{1}{2}$•|AC||BD|，使用基本不等式求出四边形ABCD的面积的最大值．
解答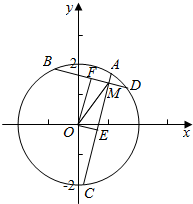 
解：如图，连接OA、OD作OE⊥AC OF⊥BD垂足分别为E、F
∵AC⊥BD
∴四边形OEMF为矩形
已知OA=OC=2，OM=$\sqrt{3}$，
设圆心O到AC、BD的距离分别为d1、d2，
则d12+d22=OM2=3．
四边形ABCD的面积为：S=$\frac{1}{2}$•|AC|（|BM|+|MD|）=$\frac{1}{2}$•|AC||BD|
=2$\sqrt{（4-{{d}_{1}}^{2}）（4-{{d}_{2}}^{2}）}$≤8-（${{d}_{1}}^{2}+{{d}_{2}}^{2}$）=5，
当且仅当d12 =d22时取等号，
故选：B．
点评 此题考查学生掌握垂径定理及勾股定理的应用，灵活运用两点间的距离公式化简求值，是一道中档题．解答关键是四边形面积可用互相垂直的2条对角线长度之积的一半来计算．
练习册系列答案
相关题目
16．
2012年10月18日全国第二届绿色运动会在池洲隆垦开幕．本次大会的主题是“绿色、低碳、环保”为大力宣传这一主题，主办方将这6个字做成灯笼悬挂在主会场（如图所示），大会结束后，要将这6个灯笼撤下来，每次撤其中一列最下面的一个，则不同的撤法种数为（ ）
2012年10月18日全国第二届绿色运动会在池洲隆垦开幕．本次大会的主题是“绿色、低碳、环保”为大力宣传这一主题，主办方将这6个字做成灯笼悬挂在主会场（如图所示），大会结束后，要将这6个灯笼撤下来，每次撤其中一列最下面的一个，则不同的撤法种数为（ ）| A． | 36 | B． | 54 | C． | 72 | D． | 90 |
3．设复数z=（1-i）n（其中i为虚数单位，n∈N*）．若z∈R，则n的最小值为（ ）
| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
20．设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的一条渐近线与抛物线y2=x的一个交点的横坐标为x0，若x0＞1，则双曲线C的离心率e的取值范围是（ ）
| A． | （1，$\frac{\sqrt{6}}{2}$） | B． | （$\sqrt{2}$，+∞） | C． | （1，$\sqrt{2}$） | D． | （$\frac{\sqrt{6}}{2}$，+∞） |
17．设曲线y=（ax-1）ex在点A（x0，y0）处的切线为l1，曲线y=（1-x）e-x在点B（x0，y1）处的切线为l2，若存在x0∈[0，$\frac{3}{2}$]，使得l1⊥l2，则实数a的取值范围是（ ）
| A． | （-∞，1] | B． | （$\frac{1}{2}$，+∞） | C． | （1，$\frac{3}{2}$） | D． | [1，$\frac{3}{2}$] |
