题目内容
19.若α为第三象限,则$\frac{cosα}{\sqrt{1-si{n}^{2}α}}$+$\frac{2sinα}{\sqrt{1-co{s}^{2}α}}$=-3.分析 α为第三象限,则sinα<0,cosα<0,化简即可.
解答 解:α为第三象限,则$\frac{cosα}{\sqrt{1-si{n}^{2}α}}$+$\frac{2sinα}{\sqrt{1-co{s}^{2}α}}$=$\frac{cosα}{-cosα}$+$\frac{2sinα}{-sinα}$=-1-2=-3,
故答案为:-3.
点评 本题考查了象限角的符号问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设a>0且a≠1,则“ab>1”是“(a-1)b>0”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
4.设集合A={x||x+1|<3},集合B={x|x2-x-6≤0},则A∩B=( )
| A. | {x|2≤x≤3} | B. | {x|-2≤x≤3} | C. | {x|-2≤x<2} | D. | {x|-4<x≤3} |
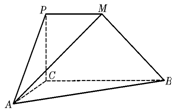 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=AC=1,BC=2,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=AC=1,BC=2,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.