Question

一个水平放置的平面图形的斜二测直观图是抛物线y²=2x的内接等腰直角三角形，则这个平面图形的面积（　　）

• A、

  2

• B、4

  2

• C、8

  2

• D、16

  2

Answer 1

考点：简单空间图形的三视图

专题：数形结合法,圆锥曲线的定义、性质与方程

分析：根据抛物线与等腰直角三角形的对称性，得出抛物线y²=2x的内接等腰直角三角形如图所示，
画出图形，结合图形，求出等腰直角△AOB的面积，利用直观图与原图形的面积关系，求出原平面图形的面积．

解答： 解：根据图形的对称性，画出该抛物线y²=2x的内接等腰直角三角形，如图所示；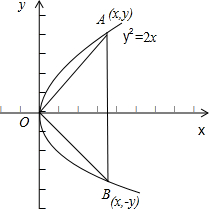
设直线OA的方程为y=x，
则由

y=x y2=2x

，
解得x=2，y=2；
等腰直角△AOB的面积为S_△AOB=

1

2

×|AB|×|x|=

1

2

×4×2=4，
∴原平面图形的面积为4×2

2

=8

2

．
故选：C．

点评：本题考查了抛物线的对称性应用问题，也考查了平面直观图与原图形的面积比的应用问题，是综合性基础题目．