题目内容
18.已知函数f(x)=xlnx-mx2有两个极值点,则实数m的取值范围是(0,$\frac{1}{2}$).分析 先求导函数,函数f(x)=x(lnx-mx)有两个极值点,等价于f′(x)=lnx-2mx+1有两个零点,等价于函数y=lnx与y=2mx-1的图象由两个交点,在同一个坐标系中作出它们的图象.由图可求得实数m的取值范围.
解答 解:由题意,y′=lnx+1-2mx
令f′(x)=lnx-2mx+1=0得lnx=2mx-1,
函数y=xlnx-mx2有两个极值点,等价于f′(x)=lnx-2mx+1有两个零点,
等价于函数y=lnx与y=2mx-1的图象有两个交点,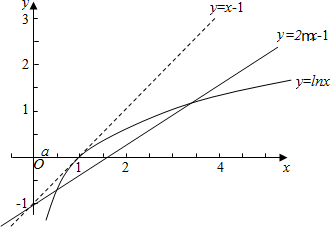 ,
,
当m=$\frac{1}{2}$时,直线y=2mx-1与y=lnx的图象相切,
由图可知,当0<m<$\frac{1}{2}$时,y=lnx与y=2mx-1的图象有两个交点,
则实数m的取值范围是(0,$\frac{1}{2}$),
故答案为:(0,$\frac{1}{2}$).
点评 本题主要考查函数的零点以及数形结合方法,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.

练习册系列答案
相关题目
13.已知函数f(x)=x3+x2f'(2),则f'(2)的值为( )
| A. | -4 | B. | 4 | C. | -3 | D. | 3 |
3.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,且$\overrightarrow a$在$\overrightarrow b$方向上的投影与$\overrightarrow b$在$\overrightarrow a$方向上的投影相等,则$|{\overrightarrow a-\overrightarrow b}|$等于( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 5 |
11.若实数x、y满足x2+y2+2x+2y+1=0,则$\frac{y}{x-1}$的取值范围是( )
| A. | (-∞,0]∪[$\frac{3}{4}$,+∞) | B. | (-∞,0]∪[$\frac{4}{3}$,+∞) | C. | [0,$\frac{3}{4}$] | D. | [0,$\frac{4}{3}$] |