题目内容

3．直线l1；x+ay+2=0和直线l2：（a-2）x+3y+6a=0，则“a=3”是“l1∥l2”的（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分也非必要条件

分析 根据充分条件和必要条件的定义结合直线平行的等价条件进行判断即可．

解答 解：若a=3，则两直线方程分别为x+3y+2=0和x+3y+18=0，满足两直线平行，即充分性成立，
若l1∥l2，
当a=0时，两直线分别为x+2=0和-2x+3y=0，此时两直线不平行，不满足条件．
当a≠0时，若两直线平行则$\frac{a-2}{1}=\frac{3}{a}$≠$\frac{6a}{2}$，
由$\frac{a-2}{1}=\frac{3}{a}$得a2-2a=3，即a2-2a-3=0，解得a=3或a=-1，
当a=-1时，$\frac{a-2}{1}=\frac{3}{a}$=$\frac{6a}{2}$，不满足条件．
则a≠-1，
即a=3，
故“a=3”是“l1∥l2”的充要条件，
故选：C

点评 本题主要考查充分条件和必要条件的判断，根据直线平行的等价条件求出a的取值范围是解决本题的关键．

练习册系列答案
相关题目
13．已知向量$\overrightarrow a$=（cosα，sinα），$\overrightarrow b$=（cosβ，sinβ），0＜α＜β＜π．
（Ⅰ）若|$\overrightarrow a$-$\overrightarrow b$|=$\sqrt{2}$，求证$\overrightarrow a$⊥$\overrightarrow b$；
（Ⅱ）设$\overrightarrow c$=（0，1），若$\overrightarrow a$+$\overrightarrow b$=$\overrightarrow c$，求α，β的值．
14．${∫}_{0}^{\frac{π}{4}}$（sinx-acosx）dx=-$\frac{\sqrt{2}}{2}$，则实数a=$\sqrt{2}$．
11．下列命题中真命题有（1），（5）
（1）已知集合A={1，2}，$B=\left\{{x\left|{x=\frac{1}{a}}\right.}\right\}$，若B⊆A，则a的值为$1或\frac{1}{2}$
（2）已知$f（x）=\left\{\begin{array}{l}（{2-a}）x+1，（{x＜1}）\\{a^x}，（{x≥1}）\end{array}\right.$（a＞0，a≠1）是R上的增函数，那么a的取值范围是（1，2）
（3）函数$f（x）=\frac{1}{x}$在定义域（-∞，0）∪（0，∞）上是减函数
（4）$\left\{{x∈N\left|{\frac{6}{6-x}∈N}\right.}\right\}=\left\{{\frac{6}{6-x}∈N\left|{x∈N}\right.}\right\}$
（5）定义在R上的函数f（x）满足f（x+2）=3f（x），当x∈[0，2]时，f（x）=x2-2x，则x∈[-4，-2]时，f（x）的最小值是$-\frac{1}{9}$．
（6）若A={x|y=x2+1}，B={y|y=x2+1}，C={（x，y）|y=x2+1}，则A∪B=C．
18．函数y=$\sqrt{x+1}$（x≥-1）的反函数为y=x2-1（x≥0）．
8．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（-2，λ），且$\overrightarrow{a}$与$\overrightarrow{b}$共线，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的值为2．
15．一元二次不等式$a{x^2}+2x+b＞0\begin{array}{l}{\;}{（a＞b）}\end{array}$的解集为$\left\{{x|x≠-\frac{1}{a}}\right\}$，则$\frac{{{a^2}+{b^2}}}{a-b}$的最小值为$2\sqrt{2}$．
12．已知f（log2x）=x+x-1
 （1）求f（1）；
（2）求函数f（x）的解析式．
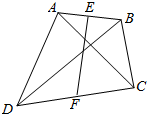13．已知，如图所示，点E、F分别为任意四边形ABCD对边AB、CD的中点，求证：$\overrightarrow{EF}$=$\frac{1}{2}$（$\overrightarrow{AC}$+$\overrightarrow{BD}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网